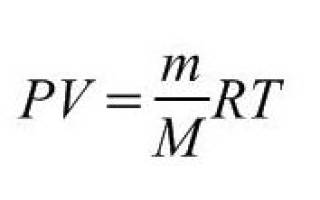Как зависит объем газа от давления

Связь между давлением, температурой, объемом и количеством молей газа («массой» газа). Универсальная (молярная) газовая постоянная R. Уравнение Клайперона-Менделеева = уравнение состояния идеального газа.

Связь между давлением, температурой, объемом и количеством молей газа («массой» газа). Универсальная (молярная) газовая постоянная R. Уравнение Клайперона-Менделеева = уравнение состояния идеального газа.

Ограничения практической применимости:

• температуры ниже -100°C и выше температуры диссоциации / разложения
• давления выше 90 бар
• вакуум глубже чем 99%

Внутри диапазона точность уравнения превосходит точность обычных современных инженерных средств измерения. Для инженера важно понимать, что для всех газов возможна существенная диссоциация или разложение при повышении температуры.

• в СИ R= 8,3144 Дж/(моль*К) — это основная (но не единственная) инженерная система измерений в РФ и большинстве стран Европы
• в СГС R= 8,3144*10 7 эрг/(моль*К) — это основная (но не единственная) научная система измерений в мире
• m-масса газа в (кг)
• M-молярная масса газа кг/моль (таким образом (m/M) — число молей газа)
• P-давление газа в (Па)
• Т-температура газа в ( °K)
• V-объем газа в м 3

Давайте решим парочку задач относительно газовых объемных и массовых расходов в предположении, что состав газа не изменяется (газ не диссоциирует) — что верно для большинства газов в указанных выше пределах применимости.

1) Доставка объемов газа одинаковой массы при одинаковом давлении но различных температурах.

Данная задача актуальна в основном, но не только, для применений и устройств, в которых напрямую измеряется объем газа.

Пусть счетчик (расходомер) в точке доставки дает объемные накопленные расходы V₁ и V₂, при температурах, соответственно, T₁ и T₂ и, пусть T₁ V₂ для одинаковых количеств газа при данных условиях. Попробуем сформулировать несколько важных на практике выводов для данного случая:

• показатели объемного счетчика газа тем «весомее», чем выше давление
• выгодно поставлять газ низкого давления
• выгодно покупать газ высокого давления

Как с этим бороться? Необходима хотя бы простая компенсация по давлению, т.е в считающее устройство должна подаваться информация с дополнительного датчика давления.

Как зависит объем газа от давления

,

где р – давление; V- объем; Т – температура;- количество идеального газа в молях;R- универсальная газовая постоянная (8,31 Дж/(Кмоль).

Если одна из величин давление, объем или температура остается постоянной, то другие две величины не могут быть изменены независимо друг от друга. Например, при постоянной температуре выполняется закон Бойля-Мариотта в виде:

Проверка закона Бойля-Мариотта.

Измерение давления воздуха в шприце при изменении объема учитывая, что температура газа постояна.

Ручной вакуумный насос

Рис 1. Общий вид установки по изучению закона Бойля – Мариотта. (1) шприц, (2) манометр (отсчет производить по черной шкале), (3) ручной вакуумный насос

В данном эксперименте закон Бойля – Мариотта подтверждается с помощью установки показанной на рисунке 1. Объем воздуха в шприце определяется следующим образом:

где rрадиус шприца, аh– расстояние от носика до поршня шприца.

Давление в системе нужно находить как:

где pатмосферное давление, аp– давление, измеренное при помощи манометра.

Порядок выполнения работы

Установите поршень шприца на отметке 50 мл.

Плотно надеть свободный конец соединительного шланга ручного вакуумного насоса на выходной патрубок шприца.

Выдвигая поршень, увеличивайте объем с шагом 5 мл, фиксируйте показания маномета по черной шкале.

Чтобы определить давление под поршнем, надо из атмосферного давления вычесть показания монометра, выраженного в паскалях. Атмосферное давление равно приблизительно 1 бар, что соответствует 100 000 Па.

Для обработки результатов измерений следует учитывать наличие воздуха в соединительном шланге. Для этого измерьте расчитайте объем соединительного шланга, измерив длину шланга рулеткой, а диаметр шланга штангенциркулем, учитывая, что толщина стенок составляет 1,5 мм.

Постройте график измеренной зависимости объема воздуха от давления.

Рассчитайте зависимость объема от давления при постоянной температуре по закону Бойля-Мариотта и постройте график.

Сравните теоретические и экспериментальные зависимости.

2133. Зависимость давления газа от температуры при постоянном объеме (закон шарля)

Рассмотрим зависимость давления газа от температуры при условии неизменного объема определенной массы газа. Эти исследования были впервые произведены в 1787 г. Жаком Александром Сезаром Шарлем (1746—1823). Газ нагревался в большой колбе, соединенной с ртутным манометром в виде узкой изогнутой трубки. Пренебрегая ничтожным увеличением объема колбы при нагревании и незначительным изменением объема при смещении ртути в узкой манометрической трубке. Таким образом, можно считать объем газа неизменным. Подогревая воду в сосуде, окружающем колбу, измеряли температуру газа по термометру Т, а соответствующее давлениер— по манометру. Наполнив сосуд тающим льдом, определяли давлениер_о, и соответствующую температуруТ_о. Было установлено, что если при 0  С давлениер_о, то при нагревании на 1  С приращение давления будет вр_о. Величинаимеет одно и то же значение (точнее, почти одно и тоже) для всех газов, а именно 1/273  C -1 . Величинуназывают температурным коэффициентом давления.

Закон Шарля позволяет рассчитать давление газа при любой температуре, если известно его давление при температуре 0  C. Пусть давление данной массы газа при 0  Cв данном объемеp_o, а давление того же газа при температуреtp. Температура меняется наt, а давления изменяется нар_оt, тогда давлениерравно:

При очень низких температурах, когда газ приближается к состоянию сжижения, а также в случае сильно сжатых газов закон Шарля неприменим. Совпадение коэффициентов и, входящих в закон Шарля и закон Гей-Люссака, не случайно. Так как газы подчиняются закону Бойля — Мариотта при постоянной температуре, тоидолжны быть равны между собой.

Подставим значение температурного коэффициента давления в формулу температурной зависимости давления:

Величину (273+t) можно рассматривать как значение температуры, отсчитанное по новой температурной шкале, единица которой такая же, как и у шкалы Цельсия, а за нуль принята точка, лежащая на 273  ниже точки, принятой за нуль шкалы Цельсия, т. е. точки таяния льда. Нуль этой новой шкалы называют абсолютным нулем. Эту новую шкалу называют термодинамической шкалой температур, гдеTt+273  .

Тогда, при постоянном объеме справедлив закон Шарля:

Зависимость давления газа от объема

Убе­дим­ся в том, что мо­ле­ку­лы газа дей­стви­тель­но рас­по­ло­же­ны до­ста­точ­но да­ле­ко друг от друга, и по­это­му газы хо­ро­шо сжи­ма­е­мы.Возь­мем шприц и рас­по­ло­жим его пор­шень при­бли­зи­тель­но по­се­ре­дине ци­лин­дра. От­вер­стие шпри­ца со­еди­ним с труб­кой, вто­рой конец ко­то­рой на­глу­хо за­крыт. Таким об­ра­зом, неко­то­рая пор­ция воз­ду­ха будет за­клю­че­на в ци­лин­дре шпри­ца под порш­нем и в труб­ке.В ци­лин­дре под порш­нем за­клю­че­но неко­то­рое ко­ли­че­ство воз­ду­ха. Те­перь по­ста­вим на по­движ­ный пор­шень шпри­ца груз. Легко за­ме­тить, что пор­шень немно­го опу­стит­ся. Это озна­ча­ет, что объем воз­ду­ха умень­шил­ся Дру­ги­ми сло­ва­ми, газы легко сжи­ма­ют­ся. Таким об­ра­зом, между мо­ле­ку­ла­ми газа име­ют­ся до­ста­точ­но боль­шие про­ме­жут­ки. По­ме­ще­ние груза на пор­шень вы­зы­ва­ет умень­ше­ние объ­е­ма газа. С дру­гой сто­ро­ны, после уста­нов­ки груза пор­шень, немно­го опу­стив­шись, оста­нав­ли­ва­ет­ся в новом по­ло­же­нии рав­но­ве­сия. Это озна­ча­ет, что сила дав­ле­ния воз­ду­ха на пор­шень уве­ли­чи­ва­ет­ся и снова урав­но­ве­ши­ва­ет воз­рос­ший вес порш­ня с гру­зом . А по­сколь­ку пло­щадь порш­ня при этом оста­ет­ся неиз­мен­ной, мы при­хо­дим к важ­но­му за­клю­че­нию.

При умень­ше­нии объ­е­ма газа его дав­ле­ние уве­ли­чи­ва­ет­ся.

Будем пом­нить при этом, что масса газа и его тем­пе­ра­ту­ра в ходе опыта оста­ва­лись неиз­мен­ны­ми. Объ­яс­нить за­ви­си­мость дав­ле­ния от объ­е­ма можно сле­ду­ю­щим об­ра­зом. При уве­ли­че­нии объ­е­ма газа рас­сто­я­ние между его мо­ле­ку­ла­ми уве­ли­чи­ва­ет­ся. Каж­дой мо­ле­ку­ле те­перь нужно прой­ти боль­шее рас­сто­я­ние от од­но­го удара со стен­кой со­су­да до дру­го­го. Сред­няя ско­рость дви­же­ния мо­ле­кул оста­ет­ся неиз­мен­ной .Сле­до­ва­тель­но, мо­ле­ку­лы газа реже уда­ря­ют­ся о стен­ки со­су­да, а это при­во­дит к умень­ше­нию дав­ле­ния газа. И, на­о­бо­рот, при умень­ше­нии объ­е­ма газа его мо­ле­ку­лы чаще уда­ря­ют­ся о стен­ки со­су­да, и дав­ле­ние газа уве­ли­чи­ва­ет­ся . При умень­ше­нии объ­е­ма газа рас­сто­я­ние между его мо­ле­ку­ла­ми умень­ша­ет­ся

Зависимость давления газа от температуры

В преды­ду­щих опы­тах тем­пе­ра­ту­ра газа оста­ва­лась неиз­мен­ной, и мы изу­ча­ли из­ме­не­ние дав­ле­ния вслед­ствие из­ме­не­ния объ­е­ма газа. Те­перь рас­смот­рим слу­чай, когда объем газа оста­ет­ся по­сто­ян­ным, а тем­пе­ра­ту­ра газа из­ме­ня­ет­ся. Масса при этом также оста­ет­ся неиз­мен­ной. Со­здать такие усло­вия можно, по­ме­стив неко­то­рое ко­ли­че­ство газа в ци­линдр с порш­нем и за­кре­пив пор­шень

Из­ме­не­ние тем­пе­ра­ту­ры дан­ной массы газа при неиз­мен­ном объ­е­ме

Чем выше тем­пе­ра­ту­ра, тем быст­рее дви­жут­ся мо­ле­ку­лы газа.

— во-пер­вых, чаще про­ис­хо­дят удары мо­ле­кул о стен­ки со­су­да;

— во-вто­рых, сред­няя сила удара каж­дой мо­ле­ку­лы о стен­ку ста­но­вит­ся боль­ше. Это при­во­дит нас к еще од­но­му важ­но­му за­клю­че­нию. При уве­ли­че­нии тем­пе­ра­ту­ры газа его дав­ле­ние уве­ли­чи­ва­ет­ся. Будем пом­нить, что дан­ное утвер­жде­ние спра­вед­ли­во, если масса и объем газа в ходе из­ме­не­ния его тем­пе­ра­ту­ры оста­ют­ся неиз­мен­ны­ми.

Хранение и транспортировка газов.

За­ви­си­мость дав­ле­ния газа от объ­е­ма и тем­пе­ра­ту­ры часто ис­поль­зу­ет­ся в тех­ни­ке и в быту. Если тре­бу­ет­ся пе­ре­вез­ти зна­чи­тель­ное ко­ли­че­ство газа из од­но­го места в дру­гое, или когда газы необ­хо­ди­мо дли­тель­но хра­нить, их по­ме­ща­ют в спе­ци­аль­ные проч­ные ме­тал­ли­че­ские со­су­ды. Эти со­су­ды вы­дер­жи­ва­ют вы­со­кие дав­ле­ния, по­это­му с по­мо­щью спе­ци­аль­ных на­со­сов туда можно за­ка­чать зна­чи­тель­ные массы газа, ко­то­рые в обыч­ных усло­ви­ях за­ни­ма­ли бы в сотни раз боль­ший объем. По­сколь­ку дав­ле­ние газов в бал­ло­нах даже при ком­нат­ной тем­пе­ра­ту­ре очень ве­ли­ко, их ни в коем слу­чае нель­зя на­гре­вать или любым спо­со­бом пы­тать­ся сде­лать в них от­вер­стие даже после ис­поль­зо­ва­ния.

Газовые законы физики.

Физика реального мира в расчетах часто сводится к несколько упрощенным моделям. Наиболее применим такой подход к описанию поведения газов. Правила, установленные экспериментальным путем, были сведены различными исследователями в газовые законы физики и послужили появлению понятия «изопроцесс». Это такое прохождение эксперимента, при котором один параметр сохраняет постоянное значение. Газовые законы физики оперируют основными параметрами газа, точнее, его физического состояния. Температурой, занимаемым объемом и давлением. Все процессы, которые относятся к изменению одного или нескольких параметров и называются термодинамическими. Понятие изостатического процесса сводится к утверждению, что во время любого изменения состояния один из параметров остается неизменным. Это поведение так называемого «идеального газа», которое, с некоторыми оговорками, может быть применено к реальному веществу. Как отмечено выше, в реальности все несколько сложнее. Однако, с высокой достоверностью поведение газа при неизменной температуре характеризуется с помощью закона Бойля-Мариотта, который гласит:

Произведение объема на давление газа — величина постоянная. Это утверждение считается верным в том случае, когда температура не изменяется.

Этот процесс носит название «изотермический». При этом меняются два из трех исследуемых параметров. Физически все выглядит просто. Сожмите надутый шарик. Температуру можно считать неизменной. А в результате внутри шара повысится давление при уменьшении объема. Величина произведения двух параметров останется неизменной. Зная исходное значение хотя бы одного из них, можно легко узнать показатели второго. Еще одно правило в списке «газовые законы физики» — изменение объема газа и его температуры при одинаковом давлении. Это называется «изобарный процесс» и описывается с помощью закона Гей-Люсака. Соотношение объема и температуры газа неизменно. Это верно при условии постоянного значения давления в данной массе вещества. Физически тоже все просто. Если хоть раз заряжали газовую зажигалку или пользовались углекислотным огнетушителем, видели действие этого закона «вживую». Газ, выходящий из баллончика или раструба огнетушителя, быстро расширяется. Его температура резко падает. Можно обморозить кожу рук. В случае с огнетушителем — образуются целые хлопья углекислотного снега, когда газ под воздействием низкой температуры быстро переходит в твердое состояние из газообразного. Благодаря закону Гей-Люсака, можно легко узнать температуру газа, зная его объем в любой момент времени. Газовые законы физики описывают и поведение при условии неизменного занимаемого объема. Такой процесс называется изохорным и описывается законом Шарля, который гласит: При неизменном занимаемом объеме, отношение давления к температуре газа остается неизменным в любой момент времени.В реальности все знают правило: нельзя нагревать баллончики от освежителей воздуха и прочие сосуды, содержащие газ под давлением. Дело кончается взрывом. Происходит именно то, что описывает закон Шарля. Растет температура. Одновременно растет давление, так как объем не меняется. Происходит разрушение баллона в момент, когда показатели превышают допустимые. Так что, зная занимаемый объем и один из параметров, можно легко установить значение второго. Хотя газовые законы физики описывают поведение некой идеальной модели, их можно легко применять для предсказания поведения газа в реальных системах. Особенно в быту, изопроцессы могут легко объяснить, как работает холодильник, почему из баллончика освежителя вылетает холодная струя воздуха, из-за чего лопается камера или шарик, как работает разбрызгиватель и так далее.

Основы МКТ.

Молекулярно-кинетическая теория вещества— способ объяснения тепловых явлений, который связывает протекание теп­ловых явлений и процессов с особенностя­ми внутреннего строения вещества и изу­чает причины, которые обусловливают теп­ловое движение. Эта теория получила при­знание лишь в XX в., хотя исходит из древнегреческого атомного учения о стро­ении вещества.

Молекулярно-кинетическая тео­рия объясняет тепловые явле­ния особенностями движения и взаимодействия микрочастиц вещества

Молекулярно-кинетическая теория основывается на законах классичес­кой механики И. Ньютона, которые позво­ляют вывести уравнение движения микро­частиц. Тем не менее в связи с огромным их количеством (в 1 см 3 вещества находится около 10 23 молекул) невозможно ежесекундно с помощью законов классичес­кой механики однозначно описать движение каждой молекулы или атома. Поэтому для построения современной теории теплоты ис­пользуют методы математической статистики, которые объясняют течение тепловых явле­ний на основании закономерностей поведе­ния значительного количества микрочастиц.

Молекулярно-кинетическая тео­рия построена на основании обобщенных уравнений движе­ния огромного количества мо­лекул.

Молекулярно-кинетическая теория объяс­няет тепловые явления с позиций пред­ставлений о внутреннем строении вещества, то есть выясняет их природу. Это более глубокая, хотя и более сложная теория, которая объясняет сущность тепловых явле­ний и обусловливает законы термодинамики.

Оба существующих подхода — термодинамический подход и молекулярно-кинетическая теория — научно доказаны и взаимно дополняют друг друга, а не проти­воречат друг другу. В связи с этим изучение тепловых явлений и процессов обычно рассматривается с позиций или моле­кулярной физики, или термодинамики, в зависимости от того, как проще изложить материал.

Термодинамический и молекулярно-кинетический подходы взаимно дополняют друг друга при объяснении тепловых явлений и процессов.

Дата добавления: 2018-02-15 ; просмотров: 2068 ; ЗАКАЗАТЬ РАБОТУ

Справочник химика 21

Химия и химическая технология

Зависимость объема газа от давления

Для практического использования этого уравнения нужно располагать зависимостью объема газа от давления. Если эти сведения даются в виде таблицы экспериментальных данных, то интеграл в уравнении (П-41) вычисляется графическим методом. Для аналитического вычисления этого интеграла нужно иметь уравнение [c.83]

Предположим, что из газовой залежи, имеющей давление 100 ат, добыто за год 100 млн. газа. При этом давлении добытое количество газа занимало в пласте объем 1 млн. при условии строгого соблюдения зависимости объема газа от давления по закону идеального газа. В действительности вследствие отклонений от этого закона при повышенных давлениях, а также вследствие несколько повышенной температуры пласта по сравнению с земной поверхностью добытый газ занимал в пласте объем несколько больший чем 1 млн. ж . Если в залежь поступит благодаря водонапорному режиму такой же объем воды, то давление газа в пласте станет лишь не намного меньше 100 ат. Уменьшение давления газа произойдет лишь вследствие некоторого поднятия уровня воды, и таким образом высота столба воды, давящего на газ, станет меньше. [c.136]

Зависимость объема газа от давления [c.94]

Вследствие сильной зависимости объема газа от давления и температуры, как правило, измеренные объемы газа необходимо отнести к единым условиям давления и температуры. Нормальными условиями считают температуру 0°С, давление 760 мм рт. ст. и отсутствие влаги. Объемы газов, которые отнесены к нормальным условиям, обозначают стоящей впереди буквой (н. мл) 270]. [c.438]

Сугцествует ряд простых способов вычисления летучестей и коэффициентов летучестей реальных газов (и компонента в смеси реальных газов) по опытным данным зависимости объема газа от давления и температуры. [c.126]

В термодинамике и физической химии функциональные зависимости часто изображают посредством графиков. В частности широко используются так называемые изотермы. Примером может служить зависимость объема газа от давления при постоянной температуре [c.11]

Зависимость объема газа от давления и температуры. Эта зависимость может быть описана уравнением состояния идеального газа (уравнением Клапейрона) [c.16]

Закон Бойля — Мариотта, описывающий зависимость объема газа от давления при постоянной температуре [c.49]

Опыты но изучению зависимости объема газа от давления показали, что почти для всех газов объем данного количества газа при постоянной температуре обратно пропорционален давлению это значит, что [c.94]

В большинстве случаев результаты эксперимента можно использовать, не прибегая к составлению эмпирических выражений. Например, экспериментальные данные по объемному поведению данного вещества при постоянной температуре наносят на график в функции давления. Через полученные точки проводят наиболее вероятную кривую. При достаточной точности экспериментальных данных и небольшом разбросе точек полученная кривая описывает объемное поведение системы с незначительной погрешностью (в противном случае следует провести тщательный анализ полученных данных). Серия таких кривых для различных температур во всем диапазоне изученных условий позволяет описать объемное поведение газа данного состава. Одновременно необходимо построить семейство кривых постоянного давления (изобары), описывающих изменение объема газов с изменением температуры. Для получения окончательных результатов кривые зависимости объема газов от давления и температуры требуют некоторого сглаживания. Такие графические представления объемного поведения являются менее трудоемкими, но не менее целесообразными, чем уравнения состояния. Как отмечалось ранее, объем газа при постоянной температуре настолько сильно изменяется с изменением давления, что графическое представление этой зависимости в широком диапазоне изменения давлений становится затруднительным. При охвате широкой области изменения давлений масштаб координаты объема должен быть очень крупным. Для устранения этой трудности был испробован ряд способов. Например, на график наносили зависимость произведения Р от давления при постоянной температуре, что существенно уменьшало область определения функции. Еще больший эффект получается от использования одной из двух специально выбранных функций объема, называемых соответственно коэффициентом сжимаемости и остаточным объемом. Каждая из этих функций характеризует объемное поведение газа на основании его отклонения от поведения идеального газа. [c.19]

Первым по времени установления (1662 г.) является закон, выражающий зависимость объема газа от давления. Его можно формулировать так [c.24]

Зависимость объема газа от давления. Закон Бойля [c.239]

Опыты по изучению зависимости объема газа от давления показали, что почти для всех газов объем некоторого количества газа при постоянной температуре обратно пропорционален давлению это значит, что в данных условиях произведение объема на давление постоянно [c.239]

Закон Р. Бойля и Э. Мариотта, выражающий зависимость объема газа от давления, формулируется следующим образом при постоянной температуре объем дан- [c.52]

Как известно, на основании законов Бойля — Мариотта и Гей-Люссака и уравнения Клапейрона зависимость объема газа от давления и температуры выражается уравнением [c.513]

Константа а характеризует силы молекулярного притяжения (Ван-дер-Ваальсовы силы), константа Ь зависит от размеров молекул газа. Графики зависимости объема газа от давления при постоянной температуре, построенные согласно этому уравнению (изотермы Ван дер-Ваальса), показывают, как меняется состояние газа при различных степенях сжатия (рис. 7). На рис. 7 точка К означает критическую точку перехода. Темпе- [c.43]

Опытным путем установлено, что в пределах точности газовых законов (для обычных условий ошибки не превышают 1%) объем определенного количества любого газа определяется только тремя величинми давлениель газа, его температурой и числом молекул во взятом количестве газа. Закон, описывающий зависимость объема газа от давления, называется законом Бойля закон, описываюпщй зависимость объема от температуры, носит название закона Шарля и Гей-Люссака закон, описывающий зависимость объема от числа молекул в данном количестве газа, называется законом Авогадро. [c.239]

Подпериод пневматической химии характеризуется исследованием газов и открытием газообразных простых тел и соединений. Кроме Бойля, открывшего известный закон зависимости объема газа от давления, с пнев-матологией связаны имена Блэка, Кавендиша, Пристли, Фонтаны и др Все эти великие химики, за исключением Бойля, которого в известном отношении можно считать предвестником следующего периода, были приверженцами теории флогистона. [c.14]

Одно из важных направлений создали химики, работавшие с газами (химики-пневматики), которые, пожалуй, скорее бессознательно, чем сознательно, поставили своей цепью изучение веш еств в газообразном состоянии. Не следует, однако, удивляться тому, что химическое изучение газов позволило открыть физические законы зависимости объема газов от давления и температуры влияние давления на объем газа было установлено Бойлем в 1660 г. и Мариоттом в 1677 г. гораздо позднее Вольта (1792) и Гей-Люссак (1802) установили влияние температуры. Эти законы вместе с законом Гей-Люссака об объемных отношениях при соединении газов составляют основу пневматологии, или науки, имеюш,ей целью изучение вещества в газообразном состоянии. В настоящее время нневматологию не рассматривают как отдельную ветвь естествознания, потому что она вошла в две очень важные науки — физику и химию, но иное положение было в XVII и XVIII вв. [c.85]

Законы идеального газа

Конспект лекции с демонстрациями

Аннотация: традиционное изложение темы, дополненное демонстрацией на компьютерной модели.

Из трех агрегатных состояний вещества наиболее простым является газообразное состояние. В газах силы, действующие между молекулами, малы и при определенных условиях ими можно пренебречь.

Газ называется идеальным, если:

— можно пренебречь размерами молекул, т.е. можно считать молекулы материальными точками;

— можно пренебречь силами взаимодействия между молекулами (потенциальная энергия взаимодействия молекул много меньше их кинетической энергии);

— удары молекул друг с другом и со стенками сосуда можно считать абсолютно упругими.

Реальные газы близки по свойствам к идеальному при:

— условиях, близких к нормальным условиям (t = 0 0 C, p = 1.03·10 5 Па);

— при высоких температурах.

Законы, которым подчиняется поведение идеальных газов, были открыты опытным путем достаточно давно. Так, закон Бойля — Мариотта установлен еще в 17 веке. Дадим формулировки этих законов.

Закон Бойля — Мариотта. Пусть газ находится в условиях, когда его температура поддерживается постоянной (такие условия называются изотермическими).Тогда для данной массы газа произведение давления на объем есть величина постоянная:

Эту формулу называют уравнением изотермы. Графически зависимость p от V для различных температур изображена на рисунке.

Свойство тела изменять давление при изменении объема называется сжимаемостью. Если изменение объема происходит при T=const, то сжимаемость характеризуется изотермическим коэффициентом сжимаемости который определяется как относительное изменение объема, вызывающее изменение давления на единицу.

Для идеального газа легко вычислить его значение. Из уравнения изотермы получаем:

Знак минус указывает на то, что при увеличении объема давление уменьшается. Т.о., изотермический коэффициент сжимаемости идеального газа равен обратной величине его давления. С ростом давления он уменьшается, т.к. чем больше давление, тем меньше у газа возможностей для дальнейшего сжатия.

Закон Гей — Люссака. Пусть газ находится в условиях, когда постоянным поддерживается его давление (такие условия называются изобарическими). Их можно осуществить, если поместить газ в цилиндр, закрытый подвижным поршнем. Тогда изменение температуры газа приведет к перемещению поршня и изменению объема. Давление же газа останется постоянным. При этом для данной массы газа его объем будет пропорционален температуре:

где V — объем при температуре t = 0 0 C, — коэффициент объемного расширения газов. Его можно представить в виде, аналогичном коэффициенту сжимаемости:

Графически зависимость V от T для различных давлений изображена на рисунке.

Перейдя от температуры в шкале Цельсия к абсолютной температуре , закон Гей — Люссака можно записать в виде:

Закон Шарля. Если газ находится в условиях, когда постоянным остается его объем (изохорические условия), то для данной массы газа давление будет пропорционально температуре:

где р — давление при температуре t = 0 0 C, — коэффициент давления. Он показывает относительное увеличение давления газа при нагревании его на 1 0 :

Закон Шарля также можно записать в виде:

Закон Авогадро: один моль любого идеального газа при одинаковых температуре и давлении занимает одинаковый объем. При нормальных условиях (t = 0 0 C, p = 1.03·10 5 Па) этот объем равен м -3 /моль.

Число частиц, содержащихся в 1 моле различных веществ, наз. постоянная Авогадро:

Легко вычислить и число n частиц в 1 м 3 при нормальных условиях:

Это число называется числом Лошмидта.

Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов, т.е.

где — парциальные давления — давления, которые бы оказывали компоненты смеси, если бы каждый из них занимал объем, равный объему смеси при той же температуре.

Уравнение Клапейрона — Менделеева. Из законов идеального газа можно получить уравнение состояния, связывающее Т, р и V идеального газа в состоянии равновесия. Это уравнение впервые было получено французским физиком и инженером Б. Клапейроном и российским учеными Д.И. Менделеевым, поэтому носит их имя.

Пусть некоторая масса газа занимает объем V₁, имеет давление p₁ и находится при температуре Т₁. Эта же масса газа в другом состоянии характеризуется параметрами V₂, p₂, Т₂ (см. рисунок). Переход из состояния 1 в состояние 2 осуществляется в виде двух процессов: изотермического (1 — 1′) и изохорического (1′ — 2).

Для данных процессов можно записать законы Бойля — Мариотта и Гей — Люссака:

Исключив из уравнений p₁ ‘ , получим

Так как состояния 1 и 2 были выбраны произвольно, то последнее уравнение можно записать в виде:

Это уравнение называется уравнением Клапейрона, в котором В — постоянная, различная для различных масс газов.

Менделеев объединил уравнение Клапейрона с законом Авогадро. Согласно закону Авогадро, 1 моль любого идеального газа при одинаковых p и T занимает один и тот же объем V_m, поэтому постоянная В будет одинаковой для всех газов. Эта общая для всех газов постоянная обозначается R и называется универсальной газовой постоянной. Тогда

Это уравнение и является уравнением состояния идеального газа, которое также носит название уравнение Клапейрона — Менделеева.

Числовое значение универсальной газовой постоянной можно определить, подставив в уравнение Клапейрона — Менделеева значения p, T и V_m при нормальных условиях:

Уравнение Клапейрона — Менделеева можно записать для любой массы газа. Для этого вспомним, что объем газа массы m связан с объемом одного моля формулой V=(m/M)V_m, где М — молярная масса газа. Тогда уравнение Клапейрона — Менделеева для газа массой m будет иметь вид:

где — число молей.

Часто уравнение состояния идеального газа записывают через постоянную Больцмана:

Исходя из этого, уравнение состояния можно представить как

где — концентрация молекул. Из последнего уравнения видно, что давление идеального газа прямо пропорционально его температуре и концентрации молекул.

Небольшая демонстрация законов идеального газа. После нажатие кнопки «Начнем» Вы увидите комментарии ведущего к происходящему на экране (черный цвет) и описание действий компьютера после нажатия Вами кнопки «Далее» (коричневый цвет). Когда компьютер «занят» (т.е. идет опыт) эта кнопка не активна. Переходите к следующему кадру, лишь осмыслив результат, полученный в текущем опыте. (Если Ваше восприятие не совпадает с комментариями ведущего, напишите!)

Вы можете убедиться в справедливости законов идеального газа на имеющейся компьютерной модели самостоятельными измерениями.