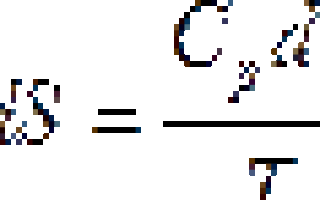Изменение свободной энергии при изменении температуры и давления

ЛЕКЦИЯ 6. 1.Зависимость энтропии от температуры

1.Зависимость энтропии от температуры. Третий закон термодинамики. Абсолютная и стандартная энтропия вещества.

2.Изменение энтропии – критерий направленности процесса. Изменение энтропии в различных процессах.

3.Термодинамические потенциалы. Полные и частные дифференциалы термодинамических потенциалов для закрытых систем. Критерии направления самопроизвольного процесса.

4.Уравнение Гиббса — Гельмгольца.

Из сказанного следует, что всякий самопроизвольный, следовательно, необратимый процесс в изолированной системе связан с увеличением энтропии. Равновесие характеризуется максимумом энтропии.

Таким образом, найден критерий возможности самопроизвольного протекания процесса, но только для изолированной системы.

Известно, что в изолированной системе нет только теплообмена с окружающей средой, но внутри нее могут идти процессы, сопровождающиеся перераспределением и превращением вещества и энергии. (Поэтому , рассматривая адиабатический процесс, в котором δQ=0 все равно нельзя считать, что ΔS =0.)

Если в объединенном уравнении первого и второго начала термодинамики вместо значения δQ подставить его выражение через теплоемкость, то получим:

Интегрирование этого выражения от абсолютного нуля до температуры Т приводит к выражению:

где S и S – энтропия вещества при абсолютом нуле и температуре Т соответственно.

Опытные данные показывают, что теплоемкости всех веществ при Т→0 резко падают до ничтожно малых величин, причем С_р уменьшается гораздо быстрее Т.

Определяя энтропии вещества при разных температурах, Нернст (1906) пришел к выводу, что изменение энтропии многих процессов, при температурах, близких к абсолютному нулю, пренебрежительно мало.

Позднее Планк (1912), Льюис и Рендал (1923) выдвинули постулат о том, что при абсолютном нуле энтропия S чистого кристаллического вещества без дефектов в кристаллической решетке равна 0. Этот постулат Планка настолько важный, что получил название третьего закона термодинамики:

При абсолютном нуле энтропия чистого кристаллического вещества без дефектов кристаллической решетки равна 0

или: Энтропия совершенного кристалла при 0 К равна нулю.

Энтропию, найденную относительно S = 0 называют абсолютной энтропией . Она, естественно, всегда положительна.

В расчетах всегда используют стандартную энтропию S 0 ₂₉₈

Стандартной называют энтропию при стандартном давлении р = 1,013 Па и температуре Т (К). Для удобства сравнения и табулирования энтропии веществ относят к базисной температуре 298 К. Рассчитывают энтропию для 1 моль вещества при неизменном агрегатном состоянии по уравнению:

или

***Интеграл от с_р тв /Т в пределах от 0 К до температуры плавления Т пл соответствует увеличению энтропии вещества в пределах области существования его в твердой области. Графически (рисунок 19) увеличение энтропии при нагревании вещество в твердом состоянии соответствует площади под кривой зависимости с_р тв /Т = f (T). При переходе в жидкое состояние при нормальной температуре плавления (Т пл ) энтропия возрастает на энтропию плавления, равную энтальпии плавления (DH пл ), деленной на Т пл в соответствии с уравнением (73). Нагреванию жидкости отвечает увеличение энтропии, вычисляемое по интегралу, в подынтегральную функцию которой входит теплоемкость жидкости (с_р ж ). Пределами интегрирования являются температура плавления (Т пл ) и температура кипения (Т кип ), т.е. область жидкого состояния. Из рисунка 19 видно, что увеличению энтропии при нагревании жидкости соответствует площадь под кривой зависимости с_р ж /Т = f (T). Кипение жидкости при постоянном давлении и температуре кипения Т кип в соответствии с уравнением (73) соответствует возрастанию энтропии на энтропию кипения, равную энтальпии кипения (DH кип ), деленной на Т кип . Нагревание газа до заданной температуры (Т) приводит к увеличению энтропии, которое рассчитывается по интегралу, в подынтегральную функцию которой входит теплоемкость жидкости (с_р ж ). Пределами интегрирования являются температура плавления (Т кип ) и заданная температура (Т). Графически (рисунок 19) увеличению энтропии при нагревании жидкости соответствует площадь под кривой зависимости с_р газ /Т = f (T).

Уравнение для вычисления абсолютной энтропии газообразного вещества будет иметь вид:

S_T =+ +++ . (85)

В таблицах стандартных величин приводятся данные – значения энтропии при 298 К и нормальном давлении. Поэтому расчет изменения энтропии в результате протекания химической реакции проводят в два этапа: вначале по уравнению (86) находят DS 0 ₂₉₈ по таблицам термодинамических величин, а затем по уравнению (87)- изменение энтропии от 0 К до Т:

D = Sn_J +Sn_¡ . (86)

D= D + . (87)

Энергия Гиббса. Энергия Гельмгольца. Направление процесса.

Чтобы дать ответ на вопрос о возможности протекания той или иной реакции, о ее направлении и глубине необходимо снова воспользоваться II – законом термодинамики, который может быть сформулирован следующим образом: любой самопроизвольно протекающий процесс, а также и химическая реакция, идет в том направлении, которое сопровождается уменьшением свободной энергии в системе (при постоянных температуре и давлении) или энергии Гельмгольца (при постоянных температуре и объеме).

Свободная энергия или Энергия Гиббса G – это та часть всей энергии системы, которую можно использовать для совершения максимальной работы.

Энергия Гельмгольца A — это та часть внутренней энергии системы, также определяющая работоспособность и может быть применена для совершения максимальной работы.

При протекании химических реакций единовременно совершаются два направления: стремление простых частиц объединиться в более сложные, а также стремление сложных частиц к распаду на более простые.

Они не зависят друг от друга и их величины противоположны, и процесс идет в сторону той реакции, при которой изменение величины больше. Разность между этими величинами определяет свободную энергию реакции (при постоянных температуре и давлении). Ее изменение в реакции определяется разностью сумм энергий Гиббса конечных продуктов реакции и исходных веществ:

При постоянных температуре и давлении изменение энергии Гиббса связано с энтальпией и энтропией следующим выражением:

Здесь изменение энергии Гиббса учитывает одновременно изменение энергетического запаса системы и степень ее беспорядка (самопроизвольность протекания процесса).

Т.к. энергия Гиббса является мерой самопроизвольности протекания процесса, то между знаком ΔG для любой реакции и ее самопроизвольным протеканием (при постоянных температуре и давлении) существуют такие зависимости:

1. Если ΔG отрицательно (ΔG 0), то реакция протекать самопроизвольно в прямом направлении не может. Однако обратная реакция идет самопроизвольно.

Энтальпийный и энтропийный факторы и направление процесса

Выясним, как функция свободной энергии зависит от изменений энтропии и энтальпии идущего процесса. Вернемся к выражению, связывающему энергию Гиббса с энтальпией и энтропией:

Без энтропийных факторов все экзотермические реакции (ΔH˂0) должны были быть самопроизвольными. Но энтропийный фактор, который определяется величиной – TΔS, может привести к росту или, наоборот, к падению способности самопроизвольного протекания.

Так, при ΔS>0, член – TΔS вносит отрицательный вклад в общую величину ΔG, следовательно он повышает возможность реакции протекать самопроизвольно.

Второе начало термодинамики. Свободная энергия Гиббса

Первое начало термодинамики дает строгое количественное описание того, как изменяется энергия любой системы в результате обмена ею с окружающей средой в форме теплоты, работы или передачи вещества. Но оно не позволяет определить условия, при которых термодинамические процессы будут протекать самопроизвольно, вплоть до наступления равновесия, а также спрогнозировать их направленность. Для выяснения этих вопросов, имеющих большой теоретический и практический интерес, используется второе начало (второй закон) термодинамики.

В термодинамических системах, как было показано ранее, наряду с уменьшением энтальпии, направленность любого физического и химического процесса определяется еще и изменением энтропии. Причем действие этих факторов часто приводит к взаимнопротивоположным результатам.

Так, при протекании химических реакций энтальпийному фактору (ΔН 0), инициирующий процессы дезагрегации молекул, т.е. распад их на более простые и меньшего размерачастицы, и увеличению вследствие этого энтропии.

Для сопоставления и сравнения действия данных факторов их необходимо выразить в одинаковых единицах измерения. Так как изменение энтальпии (ΔН) измеряется в Дж/моль, а изменение энтропии (S) – в Дж/моль ·K, необходимо умножитьSна Т. В результате этого размерность произведения Т ·Sстанет такой же, как и у изменения энтальпии, а именно:

Умножение Sна Т вполне правомерно, т.к. повышение температуры усиливает различные виды движения частиц, а значит и их беспорядок, приводя тем самым к возрастанию энтропии.

При отсутствии энтропийного фактора (S= 0) самопроизвольно могут идти процессы, сопровождающиеся положительным тепловым эффектом (ΔН 0).

В том случае, когда в системе действуют оба фактора, направление процесса определяется их суммарным влиянием, причем уменьшение энтальпии характеризует стремление системы к порядку, увеличение энтропии – к беспорядку.

Если система находится в состоянии равновесия, то, очевидно, справедливо равенство:

ΔН = ТS или ΔН – ТS = 0.

Опытным путем установлено, что для самопроизвольно идущих процессов при условии одновременного действия энтропийного (S> 0) и энтальпийного (ΔН 0, то в условиях, для которых были измереныHиTS, в прямом направлении данная реакция протекать не может. Зато осуществимой окажется обратная реакция, для которойGбудет иметь отрицательное значение.

Необходимо отметить, что отрицательные значения G (или F) определяют только принципиальную возможность самопроизвольного осуществления процесса, но ничего не говорят о скорости и условиях, необходимых для его начала.

Так, для химической реакции горения различных органических и неорганических веществ уже при комнатной температуре G 0, могут самопроизвольно протекать в прямом направлении при любых температурах, т.к.Gу них всегда будет меньше нуля. Примером такой реакции может служить гидролиз пептидов или белков.

Если для химической реакции H> 0, аS 0 иS> 0 самопроизвольному протеканию реакции в прямом направлении способствует энтропийный фактор. При низких температурах отрицательное значениеH–TSможет быть невозможно, но при нагревании – оно возможно и реакция становится осуществимой в прямом направлении. Например, тепловая денатурация белковых молекул.

Если H 3 ) и обозначают. Значенияопределены для многих соединений и приводятся в соответствующих справочниках или таблицах. Величинудля простых веществ, устойчивых при стандартных условиях, принять равной 0.

Для химических реакций:

изменение энергии Гиббса можно рассчитать следующим образом (с учетом таблицы 4)

= (3_обр.(СО_2(г)) – (3_обр.(СО_(г)) +_обр.(Fe₂O_3(к)) = 3 · (–393,5) – 3 · (–110,5) + (–822,2) = –1180,5 – (1153,7) = –26,8 (кДж).

Если  >0 отвечает принципиальной невозможности протекания процесса в прямом направлении как при Т = 298 о K, так и в других условиях. К сожалению, не существует определенных минимальных значений, за пределами которых процесс можно считать в принципе реализуемым в прямом (G 0) направлениях.

Таблица 4.Стандартные величины А/С 298 некоторых веществ (кДж/моль)

Изменение свободной энергии при изменении температуры и давления

Мы уже указывали, что свободная энергия Гиббса позволяет получать информацию двоякого рода. Во-первых, свободная энергия образования химического соединения является мерой устойчивости этого соединения. Во-вторых, изменение свободной энергии в химической реакции является мерой самопроизвольной осуществимости этой реакции. Самопроизвольное протекание возможно только для таких реакций, которые характеризуются отрицательными значениями . Однако свободная энергия Гиббса позволяет получать не только такие сведения.

Равновесие

Если система находится в состоянии динамического равновесия, то

Если реакция характеризуется большим по абсолютной величине и отрицательным по знаку значением , то можно заключить, что равновесие в данной реакции сильно сдвинуто вправо (если судить по уравнению реакции), т.е. в сторону образования продуктов. Если же свободная энергия реакции имеет большое положительное значение, то равновесие сдвинуто влево — в сторону образования реагентов.

Полезная работа

Мы уже знаем, что если в системе происходит превращение при постоянном давлении, то энергия, передаваемая в форме теплоты между системой и ее окружением, называется изменением энтальпии . Если представить это изменение энтальпии с помощью уравнения (24), то видно, что оно выражается в виде суммы двух частей

представляет собой часть изменения энтальпии, которая может использоваться для выполнения полезной работы (рис. 5.17). Остальная часть изменения энтальпии не может использоваться для выполнения работы. Она соответствует энтропийному члену

Рис. 5.17. Две составляющие, в виде суммы которых можно представить изменение энтальпии: полное изменение энергии при постоянной температуре; — свободная энергия (доступная для выполнения полезной работы); — несвободная энергия (недоступная для выполнения полезной работы).

Оценка возможности получения металлов из их оксидов по величине

Металлы можно получать, восстанавливая их оксиды (см. разд. 10.5). Для этой цели используются такие восстановители, как углерод и другие металлы. Но как можно определить, будет ли углерод или другой металл самопроизвольно восстанавливать оксид конкретного металла? Чтобы ответить на этот вопрос, рассмотрим два следующих случая.

В этом случае металл играет роль восстановителя. Он восстанавливает углерод из диоксида углерода.

В этом случае роль восстановителя играет углерод. Он восстанавливает металл из его оксида.

Нетрудно видеть, что случай 2 является обратным по отношению к случаю 1. К некоторым металлам применим случай 1, а к другим металлам-случай 2. Каким же образом можно заранее предсказать, какой случай применим к какому-либо конкретно рассматриваемому металлу? Другими словами, как предсказать-какая реакция окажется самопроизвольной: соответствующая случаю 1 или случаю 2?

Ответ заключается в сопоставлении устойчивости оксидов. Выше было указано, что мерой устойчивости соединения является свободная энергия его образования. Мы видели также, что для самопроизвольного протекания реакции изменение свободной энергии , которым она сопровождается, должно быть отрицательным, т. е. Если применить это условие к изменению свободной энергии, выраженному с помощью уравнения (25), то получится следующее условие самопроизвольного протекания реакции:

В каждом из двух рассмотренных выше случаев один из продуктов и один из реагентов являются свободными элементами. Поскольку стандартные молярные свободные энергии образования свободных элементов равны нулю, условие самопроизвольного протекания рассмотренных реакций приобретает следующий вид:

Следовательно, в обоих случаях более устойчивый оксид, т. е. оксид с более отрицательным значением свободной энергии образования должен быть продуктом, а не реагентом. Стандартные молярные свободные энергии образования оксидов, рассмотренных в примерах, приведены в табл. 5.15. Эти значения показывают, что в первом из рассмотренных выше примеров оксид магния обладает большей устойчивостью, чем диоксид углерода. Поэтому оксид магния оказывается продуктом, а не

Твблица 5.15. Стандартные молярные свободные энергии образования некоторых оксидов

реагентом. Самопроизвольно протекает прямая, а не обратная (по отношению к записанному уравнению) реакция. Другими словами, к данной реакции применим случай 1.

Второй пример оказывается более сложным. Согласно значениям приведенным в табл. 5.15, продуктом рассматриваемой реакции должен быть а не Почему же эта реакция была выбрана в качестве примера к случаю 2? Дело, оказывается, в температуре реакции. Эта реакция не протекает при 298 К. Для ее осуществления необходима более высокая температура.

Диаграммы Эллингема

Стандартные молярные свободные энергии образования оксидов металлов повышаются с температурой, а свободная энергия образования моноксида углерода, наоборот, уменьшается. Зависимость стандартной молярной свободной энергии образования этих веществ от температуры показана в графическом виде на так называемой диаграмме Эллингема (рис. 5.18). Чем выше поднимается каждая линия на этой диаграмме, тем меньше устойчивость соответствующего оксида. Так, моноксид углерода менее устойчив, чем оксид никеля (II) при температурах ниже 680 К (приблизительно), однако выше этой температуры он, наоборот, более устойчив. Поэтому

Рис. 5.18. Упрощенная диаграмма Эллингема.

реакцию восстановления оксида никеля углеродом обычно проводят при температурах выше 680 К.

Диаграммы Эллингема позволяют наглядно определять, какой оксид будет восстанавливаться в каждой конкретной реакции. При заданной температуре восстанавливаться должен тот оксид, линия которого расположена выше. Так, при 1000 К магний должен восстанавливать оксид алюминия, однако при 2000 К алюминий будет восстанавливать оксид магния. Вместе с тем, как показывает диаграмма, магний должен восстанавливать оксид цинка при любой температуре ниже 2000 К. Изломы линий на диаграмме Эллингема указывают фазовые превращения (плавление или кипение) металлов. При этих фазовых превращениях происходит резкое возрастание энтропии и соответственное изменение . Отметим также, что свободная энергия образования оксида серебра отрицательна при низких температурах, но становится положительной при повышении температуры. Изменение знака свободной энергии (т. е. достижение точки, в которой происходит при температуре 440 К.

Итак, повторим еще раз!

1. Стандартная энтальпия диссоциации связи — это изменение энтальпии, которым сопровождается разрыв одного моля связей при условии, что исходные молекулы и их фрагменты находятся в своих стандартных состояниях при температуре 298 К и давлении 1 атм.

2. Стандартная молярная энтальпия решетки — это изменение энтальпии, которым сопровождается образование одного моля кристаллического ионного соединения из входящих в него газообразных ионов в их стандартных состояниях.

3. Цикл Борна Габера — это энтальпийная диаграмма, по которой можно определить энтальпию ионной решетки соли.

4. Стандартная молярная энтальпия растворения определяется соотношением

5. Второй закон термодинамики утверждает, что полная энтропия системы и ее окружения при любых самопроизвольных процессах возрастает.

6. Для любых самопроизвольных процессов полное изменение энтропии в системе и ее окружении должно быть положительным

где .

7. Стандартное молярное изменение энтропии в химической реакции определяется выражением

8. Изменение свободной энергии Гиббса связано с суммарным изменением энтропии в системе и ее окружении соотношением

9. Изменение свободной энергии Гиббса в химической реакции является мерой самопроизвольной осуществимости этой реакции.

10. Для реакционной системы

11. Реакция может протекать самопроизвольно только при условии

12. Стандартное молярное изменение свободной энергии в химической реакции определяется выражением

13. Для системы, находящейся в состоянии динамического равновесия,

14. Изменение свободной энергии представляет собой ту часть изменения энтальпии, которая доступна для выполнения полезной работы.

15. Диаграммы Эллингема показывают зависимость стандартной молярной свободной энергии образования соединений от температуры.

Как правильно рассчитать стандартное изменение энергии Гиббса реакции

Определение изменения энергии Гиббса реакции восстановления природного минерала магнетита оксидом углерода (2)

Задача 1.
Восстановление природного минерала магнетита Fe₃O₄ оксидом углерода (2) осуществляется в производственных условиях по реакции:
Fe₃O₄(к) + CO(г) = 3FeO(к) + CO₂(г).
Определите изменение энергии Гиббса и сделайте вывод о возможности самопроизвольного протекания этого процесса при стандартных условиях.
Решение:
Изобарно-изотермический потенциал термодинамической системы или энергия Гиббса G отражает общую движущую силу процесса, т.е. обозначает ту часть полной энергии системы (Н), которая полностью и без остатка может превратиться в полезную работу (собственно химический процесс). Изменение энергии Гиббса ∆G (при Т = Const и P = Const) в сторону её уменьшения (∆G 0 х.р. =[3· ∆G 0 обрFeO(к) + ∆G 0 обрCO₂(г)] – [∆G 0 обрFe₃O₄(к) + ∆G 0 обрCO(г)].

Используя табличные значения, установим значения ∆G 0 обр продуктов реакции и реагентов:

∆G 0 обрFeO(к) = -244,3 кДж/моль;
∆G 0 обрCO₂(г) = -394,38 кДж/моль;
∆G 0 обрFe3O4(к) = -1014,20 кДж/моль;
∆G 0 обрCO(г) = -137,27 кДж/моль.

Подставив найденные значения в выражение для ∆G 0 х.р. и произведя расчеты, получим:

∆G 0 х.р. = [3·(-244,3) + (-394,38)] – [(-1014,20) + (-137,27)] = 24,19 (кДж/моль).

Расчеты показали, что ∆G 0 х.р. > 0, это означает невозможность протекания данного процесса при стандартных условиях.

Ответ: при стандартных условиях процесс самопроизвольного восстановления двуоксида железа оксидом углерода (2) неосуществим, т.к. ∆G 0 х.р. > 0.

Определение изменения энергии Гиббса реакции восстановления фосгена оксидом углерода (2)

Задача 2.
Определите стандартное изменение энергии Гиббса реакции: COCl₂(г) CO(г) + Cl₂(г), если при температуре 885 К разложилось 80% фосгена, взятого при начальном давлении 100 кПа.
Решение:
Если до начала реакции парциальное давление СОСl₂(г) было равно Р 0 = 100 кПа, за время реакции израсходовано 70% газа, то в момент установления равновесия парциальное давление оставшегося фосгена Р 0 равн:

СОСl₂(г) = Р 0 · 0,2 = 20 кПа.

Парциальные давления продуктов реакции в состоянии равновесия равны доле израсходованного фосгена, а значит,

Р 0 равнCO(г) = Р 0 равнCl₂(г) = Р 0 · 0,8 = 80 кПа.

Согласно закону действующих масс для равновесного процесса

Кравн = Р 0 равнCO(г) · Р 0 равнCl₂(г)/Р равнСОСl₂(г).

Подставим в это уравнение найденные значения парциальных равновесных давлений продуктов и реагентов и рассчитаем значение константы равновесия:

Кравн= (80 · 80)/20 = 320,0

Теперь, используя уравнение изотермы Вант-Гоффа ∆G 0 = –RTlnKp, рассчитаем изменение стандартной энергии Гиббса в состоянии равновесия при заданной температуре:

∆G 0 = (-8,31 · 885)Дж/моль · ln320,0 = -42419,89 Дж/моль = –42,4 кДж/моль.

Ответ: в состоянии равновесия при стандартных условиях изменение энергии Гиббса реакции ∆G 0 х.р.= –42,4 кДж/моль.