Закон о давлении воды

Закон Паскаля. Гидростатическое давление

Закон Паскаля для жидкости

Этот закон был открыт французским ученым Б. Паскалем в 1653 г. Его иногда называют основным законом гидростатики.

Закон Паскаля можно объяснить с точки зрения молекулярного строения вещества. В твердых телах молекулы образуют кристаллическую решетку и колеблются около своих положений равновесия. В жидкостях и газах молекулы обладают относительной свободой, они могут перемещаться друг относительно друга. Именно эта особенность позволяет давление, производимое на жидкость (или газ) передавать не только в направлении действия силы, но и во всех направлениях.

Закон Паскаля нашел широкое применение в современной технике. На законе Паскаля основана работа современных суперпрессов, которые позволяют создавать давления порядка 800 МПа. Также на этом законе построена работа всей гидроавтоматики, управляющей космическими кораблями, реактивными авиалайнерами, станками с числовым программным управлением, экскаваторами, самосвалами и т.д.

Гидростатическое давление жидкости

Гидростатическое давление внутри жидкости на любой глубине не зависит от формы сосуда, в котором находится жидкость, и равно произведению плотности жидкости, ускорения свободного падения и глубины, на которой определяется давление:

В однородной покоящейся жидкости давления в точках, лежащих в одной горизонтальной плоскости (на одном уровне), одинаковы. Во всех случаях, приведенных на рис. 1, давление жидкости на дно сосудов одинаково.

Рис.1. Независимость гидростатического давления от формы сосуда

На данной глубине жидкость давит одинаково по всем направлениям, поэтому давление на стенку на данной глубине будет таким же, как и на горизонтальную площадку, расположенную на такой же глубине.

Полное давление в жидкости, налитой в сосуд, складывается из давления у поверхности жидкости и гидростатического давления:

Давление у поверхности жидкости часто равно атмосферному давлению.

Примеры решения задач

1) Гидростатическое давление на глубине

Сила давления воды на дно куба:

где — площадь дна; ,

2) Среднее давление на боковую грань равно полусумме давлений на уровне поверхности и на уровне дна:

сила давления на стенку куба:

Из таблиц плотность воды кг/м.

Ускорение свободного падения м/с.

Переведем единицы в систему СИ: длина ребра куба см м.

Закон о давлении воды

В этом параграфе мы применим закон сохранения энергии к движению жидкости или газа по трубам. Движение жидкости по трубам часто встречается в технике и быту. По трубам водопровода подается вода в городе в дома, к местам ее потребления. В машинах по трубам поступает масло для смазки, топливо в двигатели и т. д. Движение жидкости по трубам нередко встречается и в природе. Достаточно сказать, что кровообращение животных и человека — это течение крови по трубкам — кровеносным сосудам. В какой-то мере течение воды в реках тоже является разновидностью течения жидкости по трубам. Русло реки — это своеобразная труба для текущей воды.

Как известно, неподвижная жидкость в сосуде согласно закону Паскаля передает внешнее давление по всем направлениям и во все точки объема без изменения. Однако, когда жидкость течет без трения по трубе, площадь поперечного сечения которой на разных участках различна, давление оказывается неодинаковым вдоль трубы. Выясним, почему давление в движущейся жидкости зависит от площади поперечного сечения трубы. Но сначала ознакомимся с одной важной особенностью всякого потока жидкости.

Предположим, что жидкость течет по горизонтально расположенной трубе, сечение которой в разных местах различное, например по трубе, часть которой показана на рисунке 207.

Если бы мы мысленно провели несколько сечений вдоль трубы, площади которых соответственно равны и измерили бы количество жидкости, протекающей через каждое из них за какой-то промежуток времени то мы обнаружили бы, что через каждое сечение протекло одно и то же количество жидкости. Это значит, что вся та жидкость, которая за время проходит через первое сечение, за такое же время проходит и через третье сечение, хотя оно по площади значительно меньше, чем первое. Если бы это было не так и через сечение площадью за время проходило, например, меньше жидкости, чем через сечение площадью то избыток жидкости должен был бы где-то накапливаться. Но жидкость заполняет всю трубу, и накапливаться ей негде.

Как же может жидкость, протекшая через широкое сечение, успеть за такое же время «протиснуться» через узкое? Очевидно, что для этого при прохождении узких частей трубы скорость движения должна быть больше, и как раз во столько раз, во сколько раз площадь сечения меньше.

Действительно, рассмотрим некоторое сечение движущегося столба жидкости, совпадающее в начальный момент времени с одним из сечений трубы (рис. 208). За время эта площадка переместится на расстояние которое равно где — скорость течения жидкости. Объем V жидкости, протекшей через сечение трубы, равен произведению площади этого сечения на длину

В единицу же времени протекает объем жидкости —

Объем жидкости, протекающей в единицу времени через сечение трубы, равен произведению площади поперечного сечения трубы на скорость течения.

Как мы только что видели, этот объем должен быть одним и тем же в разных сечениях трубы. Поэтому, чем меньше сечение трубы, тем больше скорость движения.

Сколько жидкости проходит через одно сечение трубы за некоторое время, столько же ее должно пройти за такое

же время через любое другое сечение.

При этом мы считаем, что данная масса жидкости всегда имеет один и тот же объем, что она не может сжаться и уменьшить свой объем (о жидкости говорят, что она несжимаема). Хорошо известно, например, что в узких местах реки скорость течения воды больше, чем в широких. Если обозначить скорость течения жидкости в сечениях площадями через то можно написать:

Отсюда видно, что при переходе жидкости с участка трубы с большей площадью сечения на участок с меньшей площадью сечения скорость течения увеличивается, т. е. жидкость движется с ускорением. А это по второму закону Ньютона означает, что на жидкость действует сила. Что это за сила?

Этой силой может быть только разность между силами давления в широком и узком участках трубы. Таким образом, в широком участке давление жидкости должно быть больше, чем в узком участке трубы.

Это же следует из закона сохранения энергии. Действительно, если в узких местах трубы увеличивается скорость движения жидкости, то увеличивается и ее кинетическая энергия. А так как мы приняли, что жидкость течет без трения, то этот прирост кинетической энергии должен компенсироваться уменьшением потенциальной энергии, потому что полная энергия должна оставаться постоянной. О какой же потенциальной энергии здесь идет речь? Если труба горизонтальна, то потенциальная энергия взаимодействия с Землей во всех частях трубы одна и та же и не может измениться. Значит, остается только потенциальная энергия упругого взаимодействия. Сила давления, которая заставляет жидкость течь по трубе, — это и есть упругая сила сжатия жидкости. Когда мы говорим, что жидкость несжимаема, то имеем лишь в виду, что она не может быть сжата настолько, чтобы заметно изменился ее объем, но очень малое сжатие, вызывающее появление упругих сил, неизбежно происходит. Эти силы и создают давление жидкости. Вот это сжатие жидкости и уменьшается в узких частях трубы, компенсируя рост скорости. В узких местах труб давление жидкости должно быть поэтому меньше, чем в широких.

В этом состоит закон, открытый петербургским академиком Даниилом Бернулли:

Давление текущей жидкости больше в тех сечениях потока, в которых скорость ее движения меньше, и,

наоборот, в тех сечениях, в которых скорость больше, давление меньше.

Как это ни покажется странным, но когда жидкость «протискивается» через узкие участки трубы, то ее сжатие не увеличивается, а уменьшается. И опыт хорошо это подтверждает.

Если трубу, по которой течет жидкость, снабдить впаянными в нее открытыми трубками — манометрами (рис. 209), то можно будет наблюдать распределение давления вдоль трубы. В узких местах трубы высота столба жидкости в манометрической трубке меньше, чем в широких. Это означает, что в этих местах давление меньше. Чем меньше сечение трубы, тем больше в ней скорость течения и меньше давление. Можно, очевидно, подобрать такое сечение, в котором давление равно внешнему атмосферному давлению (высота уровня жидкости в манометре будет тогда равна нулю). А если взять еще меньшее сечение, то давление жидкости в нем будет меньше атмосферного.

Такой поток жидкости можно использовать для откачки воздуха. На этом принципе действует так называемый водоструйный насос. На рисунке 210 изображена схема такого насоса. Струю воды пропускают через трубку А с узким отверстием на конце. Давление воды у отверстия трубы меньше атмосферного. Поэтому

газ из откачиваемого объема через трубку В втягивается к концу трубки А и удаляется вместе с водой.

Все сказанное о движении жидкости по трубам относится и к движению газа. Если скорость течения газа не слишком велика и газ не сжимается настолько, чтобы изменялся его объем, и если, кроме того, пренебречь трением, то закон Бернулли верен и для газовых потоков. В узких частях труб, где газ движется быстрее, давление его меньше, чем в широких частях, и может стать меньше атмосферного. В некоторых случаях для этого даже не требуется трубы.

Можно проделать простой опыт. Если дуть на лист бумаги вдоль его поверхности, как показано на рисунке 211, можно увидеть, что бумага станет подниматься вверх. Это происходит из-за понижения давления в струе воздуха над бумагой.

Такое же явление имеет место при полете самолета. Встречный поток воздуха набегает на выпуклую верхнюю поверхность крыла летящего самолета, и за счет этого происходит понижение давления. Давление над крылом оказывается меньше, чем давление под крылом. Именно поэтому возникает подъемная сила крыла.

1. Допустимая скорость течения нефти по трубам равна 2 м/сек. Какой объем нефти проходит через трубу диаметром 1 м в течение 1 ч?

2. Измерьте количество воды, вытекающей из водопроводного крана за определенное время Определите скорость течения воды, измерив диаметр трубы перед краном.

3. Каким должен быть диаметр трубопровода, по которому должно протекать воды в час? Допустимая скорость течения воды 2,5 м/сек.

Передача давления жидкостями и газами. Закон Паскаля

Передача давления жидкостями и газами.

Мы уже знаем, что отдельные слои и мелкие частицы жидкости и газа свободно перемещаются относительно друг друга по всем направлениям, в отличие от твердых тел. Это можно подтвердить простым опытом: если подуть на поверхность воды в стакане, то вода придет в движение.

Из-за того, что частицы газа и жидкости подвижны, давление, оказываемое на них, передаётся не только в направлении действия оказываемой силы, а в каждую точку жидкости или газа.

котором находится газ. Частицы

газа равномерно распределяются

по всему сосуду. Сосуд сверху

закрыт поршнем, который может

перемещаться вниз и вверх.

Надавим на поршень так, чтобы

он немного погрузился в сосуд и

сдавил газ. В результате частицы, рис. 1

находящиеся под поршнем, уплот-

Двигаясь, частицы газа будут перемещаться по всем направлениям и в результате этого перемещения их расположение опять станет равномерным, но уже более плотным, чем раньше (рис.1в). В результате давление газа всюду увеличится. Из этого можно сделать вывод, что дополнительное давление передается всем частицам газа. Если, например, давление на газ около самого поршня увеличится на 1 Па, то во всех точках внутри газа давление станет больше на столько же, т. е. на 1 Па. Давление газа и на поршень, и на стенки сосуда, и на дно сосуда также увеличится на 1 Па.

В 1648 году французский ученый Блез Паскаль опытным путём подтвердил то, что давление жидкости зависит от высоты её столба. Он вставил в закрытую бочку, наполненную водой, трубку диаметром 1см2, длиной 5 м и, поднявшись на балкон 2-го

Когда вода в ней поднялась до высоты

давление воды в ней увеличилось настолько, что в

крепкой дубовой бочке образовались щели, через

которые потекла вода.

Закон Паскаля гласит:

давление, производимое на жидкость или газ,

передаётся в любую точку объёма жидкости и

газа без изменений во всех направлениях.

Закон объясняется подвижностью частиц жидкос-

тей и газов во всех направлениях.

Нам нет необходимости повторять опыт

Паскаля с бочкой, но мы можем воспользоваться

трубкой Паскаля для подтверждения истинности

польется вода. Поршень давит на поверхность воды в трубке. Частицы воды, находящиеся под поршнем, уплотняясь, передают давление поршня другим, более глубоким слоям.

Из опыта следует, что давление поршня передается в каждую точку жидкости, заполняющей шар и в результате давления часть воды выталкивается

из отверстий во всех направлениях.

Если шар заполнить дымом

(рис.2б) и вдвигать поршень в трубку, то из всех

отверстий шара будут выходить

струйки дыма. Этот опыт также

подтверждает, что газы, как и

жидкости, передают производимое

на них давление во все стороны без а) б)

Закон Паскаля положен в основу устройства многих механизмов.

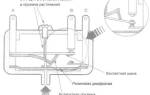
Пневматическая система водоснабжения.

Насос из водоема закачивает в бак воду, сжимающую воздушную подушку, в результате сжимаемые частицы воздуха уплотняются и, следовательно, давление увеличивается. При достижении давления воздуха 400000 Н/м2 насос отключается и прекращает закачивать воду в бак.

По Закону Паскаля давление, производимое на жидкость (или газ) передаётся в любую точку объёма жидкости (или газа) без изменений во всех направлениях. Поэтому, при открытии крана вода, под действием давления воздуха, по магистральному трубопроводу поднимается в дома.

Гидростатическое давление: формула и свойства.

Содержание

Гидростатикой называется раздел гидравлики, в котором изучаются законы равновесия жидкостей и рассматривается практическое приложение этих законов. Для того, чтобы понять гидростатику необходимо определиться в некоторых понятиях и определениях.

Закон Паскаля для гидростатики.

В 1653 году французским ученым Б. Паскалем был открыт закон, который принято называть основным законом гидростатики.

Давление на поверхность жидкости, произведенное внешними силами, передается в жидкости одинаково во всех направлениях.

Закон Паскаля легко понимается если взглянуть на молекулярное строение вещества. В жидкостях и газах молекулы обладают относительной свободой, они способны перемещаться друг относительно друга, в отличии от твердых тел. В твердых телах молекулы собраны в кристаллические решетки.

Относительная свобода, которой обладают молекулы жидкостей и газов, позволяет передавать давление производимое на жидкость или газ не только в направлении действия силы, но и во всех других направлениях.

Закон Паскаля для гидростатики нашел широкое распространение в промышленности. На этом законе основана работа гидроавтоматики, управляющей станками с ЧПУ, автомобилями и самолетами и многих других гидравлических машин.

Определение и формула гидростатического давления

Из описанного выше закона Паскаля вытекает, что:

Гидростатическое давление – это давление, производимое на жидкость силой тяжести.

Величина гидростатического давления не зависит от формы сосуда, в котором находится жидкость и определяется произведением

ρ – плотность жидкости

g – ускорение свободного падения

h – глубина, на которой определяется давление.

Для иллюстрации этой формулы посмотрим на 3 сосуда разной формы.

Во всех трёх случаях давление жидкости на дно сосуда одинаково.

Полное давление жидкости в сосуде равно

P0 – давление на поверхности жидкости. В большинстве случаев принимается равным атмосферному.

Сила гидростатического давления

Выделим в жидкости, находящейся в равновесии, некоторый объем, затем рассечем его произвольной плоскостью АВ на две части и мысленно отбросим одну из этих частей, например верхнюю. При этом мы должны приложить к плоскости АВ силы, действие которых будет эквивалентно действию отброшенной верхней части объема на оставшуюся нижнюю его часть.

Рассмотрим в плоскости сечения АВ замкнутый контур площадью ΔF, включающий в себя некоторую произвольную точку a. Пусть на эту площадь воздействует сила ΔP.

Тогда гидростатическое давление формула которого выглядит как

представлет собой силу, действующую на единицу площади, будет называться средним гидростатическим давлением или средним напряжением гидростатического давления по площади ΔF.

Истинное давление в разных точках этой площади может быть разным: в одних точках оно может быть больше, в других – меньше среднего гидростатического давления. Очевидно, что в общем случае среднее давление Рср будет тем меньше отличаться от истинного давления в точке а, чем меньше будет площадь ΔF, и в пределе среднее давление совпадет с истинным давлением в точке а.

Для жидкостей, находящихся в равновесии, гидростатическое давление жидкости аналогично напряжению сжатия в твердых телах.

Единицей измерения давления в системе СИ является ньютон на квадратный метр (Н/м 2 ) – её называют паскалем (Па). Поскольку величина паскаля очень мала, часто применяют укрупненные единицы:

килоньютон на квадратный метр – 1кН/м 2 = 1*10 3 Н/м 2

меганьютон на квадратный метр – 1МН/м 2 = 1*10 6 Н/м 2

Давление равное 1*10 5 Н/м 2 называется баром (бар).

В физической системе единицей намерения давления является дина на квадратный сантиметр (дина/м 2 ), в технической системе – килограмм-сила на квадратный метр (кгс/м 2 ). Практически давление жидкости обычно измеряют в кгс/см 2 , а давление равное 1 кгс/см 2 называется технической атмосферой (ат).

Между всеми этими единицами существует следующее соотношение:

1ат = 1 кгс/см 2 = 0,98 бар = 0,98 * 10 5 Па = 0,98 * 10 6 дин = 10 4 кгс/м 2

Следует помнить что между технической атмосферой (ат) и атмосферой физической (Ат) существует разница. 1 Ат = 1,033 кгс/см 2 и представляет собой нормальное давление на уровне моря. Атмосферное давление зависит от высоты расположения места над уровнем моря.

Измерение гидростатического давления

На практике применяют различные способы учета величины гидростатического давления. Если при определении гидростатического давления принимается во внимание и атмосферное давление, действующее на свободную поверхность жидкости, его называют полным или абсолютным. В этом случае величина давления обычно измеряется в технических атмосферах, называемых абсолютными (ата).

Часто при учете давления атмосферное давление на свободной поверхности не принимают во внимание, определяя так называемое избыточное гидростатическое давление, или манометрическое давление, т.е. давление сверх атмосферного.

Манометрическое давление определяют как разность между абсолютным давлением в жидкости и давлением атмосферным.

Рман = Рабс – Ратм

и измеряют также в технических атмосферах, называемых в этом случае избыточными.

Случается, что гидростатическое давление в жидкости оказывается меньше атмосферного. В этом случае говорят, что в жидкости имеется вакуум. Величина вакуума равняется разнице между атмосферным и и абсолютным давлением в жидкости

Рвак = Ратм – Рабс

и измеряется в пределах от нуля до атмосферы.

Свойства гидростатического давления

Гидростатическое давление воды обладает двумя основными свойствами:
Оно направлено по внутренней нормали к площади, на которую действует;
Величина давления в данной точке не зависит от направления (т.е. от ориентированности в пространстве площадки, на которой находится точка).

Первое свойство является простым следствием того положения, что в покоящейся жидкости отсутствуют касательные и растягивающие усилия.

Предположим, что гидростатическое давление направлено не по нормали, т.е. не перпендикулярно, а под некоторым углом к площадке. Тогда его можно разложить на две составляющие – нормальную и касательную. Наличие касательной составляющей из-за отсутствия в покоящейся жидкости сил сопротивления сдвигающим усилиям неизбежно привело бы к движению жидкости вдоль площадки, т.е. нарушило бы её равновесие.

Поэтому единственным возможным направлением гидростатического давления является его направление по нормали к площадке.

Если предположить что гидростатическое давление направлено не по внутренней, а по внешней нормали, т.е. не внутрь рассматриваемого объекта а наружу от него, то вследствие того, что жидкость не оказывает сопротивления растягивающим усилиям – частицы жидкости пришли бы в движение и её равновесие было бы нарушено.

Следовательно, гидростатическое давление воды всегда направлено по внутренней нормали и представляет собой сжимающее давление.

Из этого же правило следует, что если измениться давление в какой-то точке, то на такую же величину измениться давление в любой другой точке этой жидкости. В этом заключается закон Паскаля, который формулируется следующим образом: Давление производимое на жидкость, передается внутри жидкости во все стороны с одинаковой силой.

На применение этого закона основываются действие машин, работающих под гидростатическим давлением.

Ещё одним фактором влияющим на величину давления является вязкость жидкости, которой до недавнего времени приято было пренебрегать. С появлением агрегатов работающих на высоком давлении вязкость пришлось так же учитывать. Оказалось, что при изменении давления, вязкость некоторых жидкостей, таких как масла, может изменяться в несколько раз. А это уже определяет возможность использовать такие жидкости в качестве рабочей среды.

Закон Паскаля

Содержание

1. Суть закона Паскаля
2. Формула и основная величина закона Паскаля
3. Особенности давления газа и жидкости
4. Применение закона на практике
5. Что мы узнали?

• Тест по теме

Суть закона Паскаля

Закон Паскаля – давление, которое оказывается на жидкость или газ, передается в каждую точку жидкости или газа без изменений. То есть, передача давления во всех направлениях происходит одинаково.

Данный закон действителен только для жидкостей и газов. Дело в том, что молекулы жидких и газообразных веществ под давлением ведут себя совсем не так, как молекулы твердых тел. Их движение отличается друг от друга. Если молекулы жидкости и газа движутся относительно свободно, то молекулы твердых тел такой свободой не обладают. Они лишь слегка колеблются, немного отклоняясь от исходного положения. И благодаря относительно свободному передвижению молекулы газа и жидкости оказывают давление во всех направлениях.

Формула и основная величина закона Паскаля

Основной величиной в законе Паскаля является давление. Оно измеряется в Паскалях (Па). Давление (P) – отношение силы (F), которая действует на поверхность перпендикулярно, к ее площади (S). Следовательно: P=F/S.

Формулу закона Паскаля можно прочитать следующим образом: Паскаль равен силе в 1Н, которая действует на поверхность площадью 1 кв. метр – 1Па=1Н/кв.м

Особенности давления газа и жидкости

Находясь в закрытом сосуде, мельчайшие частицы жидкостей и газов – молекулы, ударяются о стенки сосуда. Так как эти частицы подвижны, то из места с более высоким давлением они способны передвигаться в место с низким давлением, т.е. в течение короткого времени оно становиться равномерным по всей поверхности занимаемого сосуда.

Для лучшего понимания закона можно провести опыт. Возьмем воздушный шарик и наполним его водой. Потом тонкой иголкой проделаем несколько отверстий. Результат не заставит себя ждать. Из дырочек начнет вытекать вода, а если шарик сжать (т.е. оказать давление), то напор каждой струи увеличиться в насколько раз, независимо оттого, в какой именно точке было оказано давление.

Этот же эксперимент можно провести с шаром Паскаля. Это круглый шар с имеющимися отверстиями с присоединенным к нему поршнем.

Рис. 1. Блез Паскаль

Определение давления жидкости на дно сосуда происходит по формуле:

p=P/S=gpSh/s

p=g ρ h

• g – ускорение свободного падения,
• ρ – плотность жидкости (кг/куб.м)
• h – глубина (высота столба жидкости)
• p – давление в паскалях.

Под водой давление зависит только от глубины и плотности жидкости. То есть в море или океане плотность будет больше при большем погружении.

Рис. 2. Давление на разных глубинах

Применение закона на практике

Многие законы физики, в том числе и закон Паскаля, применяются на практике. Например, обычный водопровод не мог бы функционировать, если бы в нем не действовал данный закон. Ведь молекулы воды в трубе движутся хаотично и относительно свободно, а значит и давление, оказываемое на стенки водопровода везде одинаковое. Работа гидравлического пресса также основана на законах движения и равновесия жидкостей. Пресс представляет собой два соединенных между собой цилиндра с поршнями. Пространство под поршнями заполняют маслом. Если на меньший поршень площадью S₂, действует сила F₂, то на больший поршень площадью S₁, действует сила F₁.

Рис. 3. Гидравлический пресс

Также можно провести эксперимент с сырым и вареным яйцом. Если острым предметом, например, длинным гвоздем, проткнуть сначала одно, а потом другое, то результат будет разным. Крутое яйцо гвоздь пройдет насквозь, а сырое разлетится вдребезги, так как для сырого яйца будет действовать закон Паскаля, а для крутого нет.

Закон Паскаля гласит, что давление во всех точках покоящейся жидкости одинаково, то есть: F₁/S₁=F₂/S₂, откуда F₂/F₁=S₂/S₁.

Сила F₂ во столько же раз больше силы F₁, во сколько раз площадь большего поршня больше площади малого.

Что мы узнали?

Основной величиной закона Паскаля, который изучают в 7 классе, является давление, которое измеряется в Паскалях. В отличие от твердых тел газообразные и жидкие вещества давят на стенки сосуда, в котором они находятся одинаково. Причиной этому молекулы, которые движутся свободно и хаотично в разных направлениях.