Давление от жидкости

Физические свойства жидкостей и газов

Жидкость в гидравлике рассматривают как сплошную среду без пустот и промежутков. Кроме того, не учитывают влияние отдельных молекул, то есть даже бесконечно малые частицы жидкости считают состоящими из весьма большого количества молекул.

Из курса физики известно, что вследствие текучести жидкости, т.е. подвижности ее частиц, она не воспринимает сосредоточенные силы. Поэтому в жидкости действуют только распределенные силы, причем эти силы могут распределяться по объему жидкости(массовые или объемные силы) или по поверхности (поверхностные силы).

Объемные (массовые) силы

К объемным (массовым) силам относятся силы тяжести и силы инерции. Они пропорциональны массе и подчиняются второму закону Ньютона.

К поверхностным силам следует отнести силы, с которыми воздействуют на жидкость соседние объемы жидкости или тела, так как это воздействие осуществляется через поверхности. Рассмотрим их подробнее.

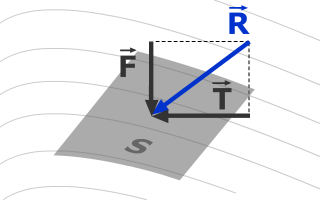
Пусть на плоскую поверхность площадью S под произвольным углом действует сила R

Силу R можно разложить на тангенциальную Т и нормальную F составляющие.

Тангенциальная составляющая называется силой трения Т и вызывает в жидкости касательные напряжения (или напряжения трения):

= T / S

Единицей измерения касательных напряжений в системе СИ является Паскаль (Па) — ньютон, отнесенный к квадратному метру (1 Па = 1 Н/м 2 ).

Давление в жидкости

Нормальная сила F называется силой давления и вызывает в жидкости нормальные напряжения сжатия, которые определяются отношением:

Нормальные напряжения, возникающие в жидкости под действием внешних сил, называются гидромеханическим давлением или просто давлением.

Системы отсчета давления

Рассмотрим системы отсчета давления. Важным при решении практических задач является выбор системы отсчета давления (шкалы давления). За начало шкалы может быть принят абсолютный нуль давления. При отсчете давлений от этого нуля их называют абсолютными — P_абс.

Однако, как показывает практика, технические задачи удобнее решать, используя избыточные давления P_изб, т.е. когда за начало шкалы принимается атмосферное давление.

Давление, которое отсчитывается «вниз» от атмосферного нуля, называется давлением вакуума P_вак, или вакуумом.

где P_атм — атмосферное давление, измеренное барометром.

Связь между абсолютным давлением P_абс и давлением вакуума P_вак можно установить аналогичным путем:

И избыточное давление, и вакуум отсчитываются от одного нуля (P_атм), но в разные стороны.

Таким образом, абсолютное, избыточное и вакуумное давления связаны и позволяют пересчитать одно в другое.

Единицы измерения давления

Практика показала, что для решения технических (прикладных) задач наиболее удобно использовать избыточные давления. Основной единицей измерения давления в системе СИ является паскаль (Па), который равен давлению, возникающему при действии силы в 1 Н на площадь размером 1 м2 (1 Па = 1 Н/м2).

Однако чаще используются более крупные единицы: килопаскаль (1 кПа = 10 3 Па) и мегапаскаль (1 МПа = 10 6 Па).

В технике широкое распространение получила внесистемная единица — техническая атмосфера (ат), которая равна давлению, возникающему при действии силы в 1 кгс на площадь размером 1 см 2 (1 ат = 1 кгс/см 2 ).

Соотношения между наиболее используемыми единицами следующие:

10 ат = 0,981 МПа ≈ 1 МПа или 1 ат = 98,1 кПа ≈ 100 кПа.

В зарубежной литературе используется также единица измерения давления бар

В каких ещё единицах измеряется давление, можно посмотреть здесь

Рассмотрим некоторые свойства жидкостей, которые оказывают наиболее существенное влияние на происходящие в них процессы и поэтому учитываются при расчетах гидравлических систем.

Плотность и удельный вес

Важнейшими характеристиками механических свойств жидкости являются ее плотность и удельный вес. Они определяют «весомость» жидкости.

Под плотностью ρ (кг/м 3 ) понимают массу жидкости m, заключенную в единице ее объема V, т.е.

Вместо плотности в формулах может быть использован также удельный вес γ (Н/м 3 ), т.е. вес G = m⋅g, приходящийся на единицу объема V:

γ = G / V = m⋅g / V = ρ⋅g

Изменения плотности и удельного веса жидкости при изменении температуры и давления незначительны, и в большинстве случаев их не учитывают.

Плотности наиболее употребляемых жидкостей и газов (кг/м 3 ):

Вязкость — это способность жидкости сопротивляться сдвигу, т. е. свойство, обратное текучести (более вязкие жидкости являются менее текучими). Вязкость проявляется в возникновении касательных напряжений (напряжений трения).

Рассмотрим слоистое течение жидкости вдоль стенки (рисунок)

В этом случае происходит торможение потока жидкости, обусловленное ее вязкостью. Причем скорость движения жидкости в слое тем ниже, чем ближе он расположен к стенке. Согласно гипотезе Ньютона касательное напряжение, возникающее в слое жидкости на расстоянии у от стенки, определяется зависимостью:

Закон трения Ньютона

где dv/dy — градиент скорости, характеризующий интенсивность нарастания скорости v при удалении от стенки (по оси у), μ ‑ динамическая вязкость жидкости.

Течения большинства жидкостей, используемых в гидравлических системах, подчиняются закону трения Ньютона, и их называют ньютоновскими жидкостями.

Однако следует иметь в виду, что существуют жидкости, в которых закон Ньютона в той или иной степени нарушается. Такие жидкости называют неньютоновскими.

Величина μ, входящая в формулу (динамическая вязкость жидкости), измеряется в Па⋅с либо в пуазах 1 П = 0.1 Па⋅с. Пуа́з (обозначение: П, до 1978 года пз; международное — P; от фр. poise) — единица динамической вязкости в системе единиц СГС. Один пуаз равен вязкости жидкости, оказывающей сопротивление силой в 1 дину взаимному перемещению двух слоев жидкости площадью 1 см², находящихся на расстоянии 1 см друг от друга и взаимно перемещающихся с относительной скоростью 1 см/с.

1 П = 1 г / (см·с) = 0,1 Н·с/м²

Единица названа в честь Ж. Л. М. Пуазёйля. Пуаз имеет аналог в системе СИ — паскаль-секунда (Па·c).

Вода при температуре 20 °C имеет вязкость 0,01002 П, или около 1 сантипуаза.

Однако на практике более широкое применение нашла

Единицей измерения последней в системе СИ является м 2 /с или более мелкая единица — см 2 /с, которую принято называть стоксом, 1 Ст = 1 см 2 /с. Для измерения вязкости также используются сантистоксы: 1 сСт = 0,01 Ст.

Вязкость жидкостей существенно зависит от температуры, причем вязкость капельных жидкостей с повышением температуры падает, а вязкость газов — растет (см. рисунок).

Это объясняется тем, что в капельных жидкостях, где молекулы расположены близко друг к другу, вязкость обусловлена силами молекулярного сцепления. Эти силы с ростом температуры ослабевают, и вязкость падает. В газах молекулы располагаются значительно дальше друг от друга. Вязкость газа зависит от интенсивности хаотичного движения молекул. С ростом температуры эта интенсивность растет и вязкость газа увеличивается.

Вязкость жидкостей зависит также от давления, но это изменение незначительно, и в большинстве случаев его не учитывают.

Сжимаемость

Сжимаемость — это способность жидкости изменять свой объем под действием давления. Сжимаемость капельных жидкостей и газов существенно различается. Так, капельные жидкости при изменении давления изменяют свой объем крайне незначительно. Газы, наоборот, могут значительно сжиматься под действием давления и неограниченно расширяться при его отсутствии.

Для учета сжимаемости газов при различных условиях могут быть использованы уравнения состояния газа или зависимости для политропных процессов.

Сжимаемость капельных жидкостей характеризуется коэффициентом объемного сжатия β_р (Па -1 ):

где dV — изменение объема под действием давления; dр — изменение давления; V — объем жидкости.

Знак «минус» в формуле обусловлен тем, что при увеличении давления объем жидкости уменьшается, т.е. положительное приращение давления вызывает отрицательное приращение объема.

При конечных приращениях давления и известном начальном объеме V можно определить конечный объем жидкости:

а также ее плотность

Величина, обратная коэффициенту объемного сжатия β_р, называется объемным модулем упругости жидкости (или модулем упругости) К = 1/ β_р (Па).

Эта величина входит в обобщенный закон Гука, связывающий изменение давления с изменением объема

Модуль упругости капельных жидкостей изменяется при изменении температуры и давления. Однако в большинстве случаев K считают постоянной величиной, принимая за нее среднее значение в данном диапазоне температур или давлений.

Модули упругости некоторых жидкостей (МПа):

Температурное расширение

Способность жидкости изменять свой объем при изменении температуры называется температурным расширением. Оно характеризуется коэффициентом температурного расширения β_t:

где dT- изменение температуры; dV- изменение объема под действием температуры; V — объем жидкости.

При конечных приращениях температуры:

Как видно из формул, с увеличением температуры объем жидкости возрастает, а плотность уменьшается.

Коэффициент температурного расширения жидкостей зависит от давления и температуры:

То есть при разных условиях коэффициент температурного расширения изменился в 50 раз. Однако на практике обычно принимают среднее значение в данном диапазоне температур и давления.Например, для минеральных масел β_t ≈ 800·10 -6 1/град.

Газы весьма значительно изменяют свой объем при изменении температуры. Для учета этого изменения используют уравнения состояния газов или формулы политропных процессов.

Испаряемость

Любая капельная жидкость способна изменять свое агрегатное состояние, в частности превращаться в пар. Это свойство капельных жидкостей называют испаряемостью. В гидравлике наибольшее значение имеет условие, при котором начинается интенсивное парообразование по всему объему — кипение жидкости.

Для начала процесса кипения должны быть созданы определенные условия (температура и давление). Например, дистиллированная вода закипает при нормальном атмосферном давлении и температуре 100°С. Однако это является частным случаем кипения воды. Та же вода может закипеть при другой температуре, если она будет находиться под воздействием другого давления, т. е. для каждого значения температуры жидкости, используемой в гидросистеме, существует свое давление, при котором она закипает.

Давление при котором жидкость закипает, называют давлением насыщенных паров (p_н.п.).

Величина p_н.п. всегда приводится как абсолютное давление и зависит от температуры.

Для примера на рисунке приведена зависимость давления насыщенных паров воды от температуры.

На графике выделена точка А, соответствующая температуре 100°С и нормальному атмосферному давлению р_а. Если на свободной поверхности воды создать более высокое давление р₁, то она закипит при более высокой температуре Т₁ (точка В на рисунке). И наоборот, при малом давлении р₂ вода закипает при более низкой температуре Т₂ (точка С).

Растворимость газов

Многие жидкости способны растворять в себе газы. Эта способность характеризуется количеством растворенного газа в единице объема жидкости, различается для разных жидкостей и изменяется с увеличением давления.

Относительный объем газа, растворенного в жидкости до ее полного насыщения, можно считать по закону Генри прямо пропорциональным давлению, то есть:

Гидростатическое давление

Калькулятор находит неизвестные величины по заданным, используя формулу давления столба жидкости.

Калькулятор ниже предназначен для расчета неизвестной величины по заданным, используя формулу давления столба жидкости.
Сама формула:

Калькулятор позволяет найти

• давление столба жидкости по известным плотности жидкости, высоте столба жидкости и ускорению свободного падения
• высоту столба жидкости по известным давлению жидкости, плотности жидкости и ускорению свободного падения
• плотность жидкости по известным давлению жидкости, высоте столба жидкости и ускорению свободного падения
• ускорение свободного падения по известным давлению жидкости, плотности жидкости и высоте столба жидкости

Вывод формул для всех случаев тривиален. Для плотности по умолчанию используется значение плотности воды, для ускорения свободного падения — земное ускорение, и для давления — величина равная давлению в одну атмосферу. Немного теории, как водится, под калькулятором.

Гидростатическое давление

Гидростатическое давление — давление столба воды над условным уровнем.

Формула гидростатического давления выводится достаточно просто

Из этой формулы видно, что давление не зависит от площади сосуда или его формы. Оно зависит только от плотности и высоты столба конкретной жидкости. Из чего следует, что, увеличив высоту сосуда, мы можем при небольшом объеме создать довольно высокое давление.
В 1648 г. это продемонстрировал Блез Паскаль. Он вставил в закрытую бочку, наполненную водой, узкую трубку и, поднявшись на балкон второго этажа, влил в эту трубку кружку воды. Из-за малой толщины трубки вода в ней поднялась до большой высоты, и давление в бочке увеличилось настолько, что крепления бочки не выдержали, и она треснула.

Также это приводит к такому явлению как гидростатический парадокс.

Гидростатический парадокс — явление, при котором сила весового давления налитой в сосуд жидкости на дно сосуда может отличаться от веса налитой жидкости. В сосудах с увеличивающимся кверху поперечным сечением сила давления на дно сосуда меньше веса жидкости, в сосудах с уменьшающимся кверху поперечным сечением сила давления на дно сосуда больше веса жидкости. Сила давления жидкости на дно сосуда равно весу жидкости лишь для сосуда цилиндрической формы.

На картинке вверху давление на дно сосуда по всех случаях одинакова и не зависит от веса налитой жидкости, а только от ее уровня. Причина гидростатического парадокса состоит в том, что жидкость давит не только на дно, но и на стенки сосуда. Давление жидкости на наклонные стенки имеет вертикальную составляющую. В расширяющемся кверху сосуде она направлена вниз, в сужающемся кверху сосуде она направлена вверх. Вес жидкости в сосуде будет равен сумме вертикальных составляющих давления жидкости по всей внутренней площади сосуда

СИЛА ДАВЛЕНИЯ В ЖИДКОСТИ. ДАВЛЕНИЕ

Гидростатика изучает жидкости, кото­рые находят- ся в состоянии равновесия.

Жидкости имеют особые механические свойства:

— малая сжимаемость (жидкость практически сохраняет свой объём даже при больших внешних силах давления),

— в земных условиях жидкость принимает форму того сосуда, в котором она находится.

В жидкости действуют силы упруго­сти, которые направлены перпендикуляр­но к любой твердой поверхности или гра­нице. Эти силы называются с и л а м и д а в л е н и я.

Силы давления распределяются по по­верхности, на которую они действуют (рис. 94).

Д а в л е н и е м называется физическая величина, равная отношению модуля си­лы давления к площади поверхности, на которую сила давления действует:

, (V.1)

где Р — давление,

S — площадь поверхности.

Единица давления в СИ — 1 паскаль:

[Р] = 1 Па = 1 Н/м 2 .

Единица давления в системе СГС — 1 дин/см 2 .

На практике часто используют вне­системные единицы давления:

— 1 миллиметр ртутного столба,

1 мм рт. cт. » 133 Па;

— 1 физическая атмосфера (обозна­чается 1 атм),

1 атм = 760 мм рт. ст.= 1,013× 10 5 Па;

— 1 техническая атмосфера (обозначается 1 ат),

1 ат = 1 кгс/см 2 = 9,8×10 4 Па.

2. ЗАКОН ПАСКАЛЯ

Если жидкость находится в равнове­сии и к повер- хности жидкости приложе­ны внешние силы, то выполняется закон Паскаля: давление, которое производят внеш­ние силы на поверхность жидкости, пере­даётся во все точки жидкости без изме­нения.

Рассмотрим гидравлическую машину, действие которой основано на законе Паскаля.

Гидравлическая машина состоит из двух цилинд- ров, которые соединены между собой (рис. 95). В цилиндрах под поршнями находится жидкость (масло). Площадь поршня в первом цилиндре — S₁, площадь поршня во втором цилинд­ре — S₂ (S₁ Р_BB`.

Из закона Паскаля и формулы (V.4) следует условие равновесия жидкости: давление на любом горизонтальном уровне жидкости, которая находится в равновесии, одинаково во всех точках на этом уровне.

Например (см. рис. 96):

— если на открытую поверхность жидкости действует внешнее давление (например,атмосферное давление Р_ат), то полное давление в любой точ­ке жидкости равно

где Р_ат — атмосферное давление;

r_ж×g × h — гидростатическое давление столба жид­кости

высотой h над уровнем, которому принадлежит данная точка.

4. СООБЩАЮЩИЕСЯ СОСУДЫ

С о о б щ а ю щ и м и с я с о с у д а м и называются два или несколько сосудов, которые соединяются друг с другом (рис. 97).

С в о б о д н о й п о в е р х н о с т ь ю жидкости называется поверхность жидко­сти, которая не соприкасается со стенка­ми сосуда.

Из закона Паскаля и формулы (V.4) следует, что свободная поверхность одно­родной жидкости (r₁ = r₂) в состоянии равновесия в сообщающихся сосу­дах устанавливается на одном горизонтальном

уровне (см. рис. 97).

Если в сообщающихся сосудах находятся несмешивающиеся жидкости с разными плотностями (r₁ ¹ r₂), то свободные поверхности жидкостей в разных сосудах могут находиться на разных

уровнях (см. рис. 98):

(V.6)

5. ЗАКОН АРХИМЕДА

Определим силу F¢, с которой тело рас­тягивает пружину, если:

— тело находится в воздухе (рис. 99, а).

— тело находится в жидкости (рис. 99, б).

В первом случае эта сила равна

Во втором случае сила, с которой те­ло растягивает пружину, уменьшается:

Таким образом, равнодействующая всех сил давления жидкости на твердое тело — выталкивающая сила — направ­лена вертикально вверх и равна

где Н × S― объём жидкости, вытесненной телом (V_выт.ж.).

Объём жидкости, вытесненной телом (V_выт.ж.) равен:

―объёму тела, если всё тело нахо­дится в жидкости (рис. 101, а):

— объёму той части тела, которая на­ходится в жидкости (рис. 101, б ).

Формула (V.9) — это математическое выражение закона Архимеда:

На тело, погружённое в жидкость (или газ), действует выталкивающая си­ла, направленная вертикально вверх и равная весу жидкости, вытесненной те­лом.

Выталкивающая сила приложена в центре объёма жидкости, вытесненного телом.

. ОТВЕТЬТЕ НА ВОПРОСЫ:

1. В чём различие понятий: сила давления и давление?

2. Какое соотношение между единицами дав­ления?

3. Какой закон лежит в основе действия гидравлической машины?

4. Что является причиной гидростатического давления?

VI. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ

В природе часто встречается движе­ние, которое повторяется во времени. На­пример, движение точки колеса при рав­номерном вращении, движение точек натянутой струны, движение маятника ме­ханических часов (рис. 102). Это примеры периодического движения.

Периодическим называется такое движение, отдельные этапы которого точно повторяются через определенный интер­вал времени.

Частный случай периодического движения — это колебательное движение. Такое движение может совершать тело или система тел, которые имеют положе­ние устойчивого равновесия.

К о л е б а т е л ь н о е д в и ж е н и е — это такое периодическое движение, при котором тело или система тел отклоняются от некоторого положе­ния равновесия то в одну, то в другую сторону.

Среди примеров, показанных на рис. 102, колебательное движение (или просто колебания) совершают натянутая струна и маятник часов (рис. 102, б, в).

Шарик на вогнутой поверхности так­же будет совершать колебательное движение относительно положения устойчи­вого равновесия, если в начальный момент он будет выведен из положения равновесия и предоставлен самому себе (см. рис. 88).

Колебания системы тел могут быть свободными и вынужденными.

С в о б о д н ы м и, или с о б с т в е н н ы м и, назы­ваются колебания системы тел, на кото­рую не действуют периодические внешние силы.

Свободные колебания совершают на­тянутая струна и шарик на вогнутой по­верхности, если их отклонить от положе­ния равновесия и предоставить самим се­бе.

В ы н у ж д е н н ы м и называются колеба­ния системы тел, на которую действует периодическая внешняя сила.

1. ХАРАКТЕРИСТИКИ КОЛЕБАТЕЛЬНОГО ДВИЖЕНИЯ.

П е р и о д (обозначается Т) — это вре­мя одного полного колебания (одного цикла колебания). В системах единиц СИ и СГС период измеряется в секундах.

Ч а с т о т а (обозначается f ) — это ве­личина, обратная периоду и равная числу колебаний за одну секунду:

Единица измерения частоты колебаний в системах СИ и СГС называется герц:

[ f ] = 1 Гц = 1 с -1 .

При частоте в один герц тело или система тел совершают одно колебание за одну секунду.

На практике часто используют единицы измерения частоты:

1 килогерц = 1 кГц = 10 3 Гц,

1 мегагерц = 1 мГц = 10 6 Гц.

Если система тел совершает свобод­ные (собственные) колебания, то часто­та таких колебаний называется собствен­ной частотой.

Смещение (обозначается х) — это величина отклонения тела или системы тел от положения устойчивого равнове­сия. Наиболее часто смещение измеряет­ся в единицах длины:

в системе СИ [х] = 1 м,

в системе СГС [х] = 1 см.

Функция зависимости смещения от времени x (t) полностью описывает данное колебательное движение.

Рассмотрим наиболее простой вид ко­лебаний — гармонические колебания.

Г а р м о н и ч е с к и м и называются та­кие колебания, при которых смещение изменяется со временем по закону синуса или косинуса:

В формуле (VI. 1) содержатся следующие характеристики гармонических колеба­ний.

А м п л и т у д а:

(обозначается А) — это величина максимального смещения; из­меряется в единицах длины.

Ц и к л и ч е с к а я ч а с т о т а:

(обозначает­ся w) — греческая буква «омега») — это величина, связанная с частотой и перио­дом соотношением

Единица измерения циклической часто­ты — радиан в секунду

Ф а з а к о л е б а н и я:

(обозначается j — греческая буква «фи»)

Н а ч а л ь н а я ф а з а:

(обозначается j) — это фаза колебания в момент времени t = 0.

Если начальная фаза равна нулю j = 0, то в начальный момент времени t = 0 смещение тела равно нулю х = 0, т. е. тело находится в точке положения равновесия.

Фаза и начальная фаза измеряются в радианной мере угла.

Некоторые перечисленные характери­стики колебаний удобно показать на гра­фике зависимости смещения от фазы. Пусть у нас есть две системы тел, кото­рые совершают гармонические колебания с одинаковой амплитудой и частотой, но с разными начальными фазами: для пер­вой колебательной системы начальная фаза равна нулю:

a для второй системы начальная фаза от­лична от нуля

Пусть в данном случае аргументом функ­ции смещения будет фаза первой колеба­тельной системы j = wt. На рис. 103 по­казаны графики этих двух колебаний — две синусоиды.

Рассмотрим, как параметры колеба­ний связаны с геометрическими характе­ристиками графиков на рис. 103.

Для колебательного движения х₁(j), например в точке n, смещение х _n равно длине отрезка ND, фаза j _n равна длине отрезка фазовой оси ОD. Разность фаз между точками с одинаковым смеще­нием М и N, равная 2p, соответствует периоду колебания Т. Максимальное сме­щение равно амплитуде А.

На рис. 103 видно также, что синусои­да х₁(j) начинается в точке х₁= 0 (в точке положения равнове- сия) при j = 0, что соответствует начальному моменту времени t = 0. Синусоида х₂(j) приходит в положение х = 0 только через некоторое время, которому соответ- ствует отрезок фазовой оси ОС. Длина этого отрезка по модулю равна начальной фазе: ОС = j.

Если смещение точки при гармонических коле­баниях изменяется по закону сину­са (VI. 1), то скорость движения точки, которая совершает колебательное движение, изменяется по закону:

. ОТВЕТЬТЕ НА ВОПРОСЫ:

1. В чём различие периодического и колеба­тельного движений?

2. Что такое собственная частота колебаний?

3 Какими характеристиками полностью опре­деляется гармоническое колебание?

4. Что есть общего и различного в параметрах колебаний: а) смещение и амплитуда? б) ча­стота и циклическая частота? в) фаза и начальная фаза?

5. Как выразить фазу через период колеба­ний?

6. Как изменятся параметры гармонических колеба- ний, если уравнение (VI.1) записать не через синус, а через косинус?

Жидкость, давление, скорость – основы закона сантехники

Главная страница » Жидкость, давление, скорость – основы закона сантехники

Сантехника, казалось бы, не даёт особого повода вникать в дебри технологий, механизмов, заниматься скрупулёзными расчётами для выстраивания сложнейших схем. Но такое видение – это поверхностный взгляд на сантехнику. Реальная сантехническая сфера ничуть не уступает по сложности процессов и, также как многие другие отрасли, требует профессионального подхода. В свою очередь профессионализм – это солидный багаж знаний, на которых основывается сантехника. Окунёмся же (пусть не слишком глубоко) в сантехнический учебный поток, дабы приблизиться на шаг к профессиональному статусу сантехника.

Закон Паскаля

Фундаментальная основа современной гидравлики сформировалась, когда Блезу Паскалю удалось обнаружить, что действие давления жидкости неизменно в любом направлении. Действие жидкостного давления направлено под прямым углом к площади поверхностей.

Если измерительное устройство (манометр) разместить под слоем жидкости на определенной глубине и направлять его чувствительный элемент в разные стороны, показания давления будут оставаться неизменными в любом положении манометра.

То есть давление жидкости никак не зависит от смены направления. Но давление жидкости на каждом уровне зависит от параметра глубины. Если измеритель давления перемещать ближе к поверхности жидкости, показания будут уменьшаться.

Соответственно, при погружении измеряемые показания будут увеличиваться. Причём в условиях удвоения глубины, параметр давления также удвоится.

Закон Паскаля наглядно демонстрирует действие давления воды в самых привычных условиях для современного быта

Отсюда логичный вывод: давление жидкости следует рассматривать прямо пропорциональной величиной для параметра глубины.

В качестве примера рассмотрим прямоугольный контейнер размерами 10х10х10 см., который заполнен водой на 10 см глубины, что по объёмной составляющей будет равняться 10 см 3 жидкости.

Этот объём воды в 10 см 3 весит 1 кг. Используя имеющуюся информацию и уравнение для расчёта, несложно вычислить давление на дне контейнера.

Например: вес столба воды высотой 10 см и площадью поперечного сечения 1 см 2 составляет 100 г (0,1 кг). Отсюда давление на 1 см 2 площади:

P = F / S = 100 / 1 = 100 Па (0,00099 атмосферы)

Если глубина столба воды утроится, вес уже будет составлять 3 * 0,1 = 300 г (0,3 кг), и давление, соответственно увеличится втрое.

Таким образом, давление на любой глубине жидкости равноценно весу столба жидкости на этой глубине, поделённому на площадь поперечного сечения столба.

Давление водяного столба: 1 — стенка контейнера для жидкости; 2 — давление столба жидкости на донную часть сосуда; 3 — давление на основание контейнера; А, С — области давления на боковины; В — прямой водяной столб; Н — высота столба жидкости

Объем жидкости, создающей давление, называется гидравлический напор жидкости. Давление жидкости благодаря гидравлическому напору, также остаётся зависимым от плотности жидкости.

Сила тяжести

Гравитация — одна из четырех сил природы. Мощь гравитационной силы между двумя объектами зависит от массы этих объектов. Чем массивнее объекты, тем сильнее гравитационное притяжение.

Когда выливается вода из контейнера, гравитация Земли притягивает воду к земной поверхности. Можно наблюдать тот же самый эффект, если на разных высотах разместить два ведра воды и соединить их трубкой.

Достаточно задать ход жидкости в трубке из одного ведра в другой, после чего сработает сила гравитации, и процесс перелива продолжится самопроизвольно.

Гравитация, приложенные силы и атмосферное давление являются статическими факторами, которые в равной степени относятся к жидкостям, находящимся в покое или в движении.

Силы инерции и трения являются динамическими факторами, которые действуют только на жидкости в движении. Математическая сумма силы тяжести, приложенной силы и атмосферного давления, представляет собой статическое давление, полученное в любой зоне жидкости и в любой момент времени.

Статическое давление

Статическое давление существует в дополнение к любым динамическим факторам, которые также могут присутствовать одновременно. Закон Паскаля гласит:

Давление, создаваемое жидкостью, действует равноценно по всем направлениям и под прямым углом к содержащимся поверхностям.

Это определение касается только жидкостей, находящихся в полном покое или практически недвижимых. Определение справедливо также только для факторов, составляющих статический гидравлический напор.

Очевидно: когда скорость движения становится фактором, в расчёт берётся направление. Сила, привязанная к скорости, также должна иметь направление. Поэтому закон Паскаля, как таковой, не применяется к динамическим факторам мощности потока жидкости.

Скорость движения потока зависит от многих факторов, включая послойное разделение жидкостной массы, а также сопротивление, создаваемое разными факторами

Динамические факторы инерции и трения привязаны к статическим факторам. Скоростной напор и потери давления привязаны к гидростатическому напору жидкости. Однако часть скоростного напора всегда может быть преобразована в статический напор.

Сила, которая может быть вызвана давлением или напором при работе с жидкостями, необходима, чтобы начать движение тела, если оно находится в состоянии покоя, и присутствует в той или иной форме, когда движение тела заблокировано.

Поэтому всякий раз, когда задана скорость движения жидкости, часть ее исходного статического напора используется для организации этой скорости, которая в дальнейшем существует уже как напорная скорость.

Объем и скорость потока

Объем жидкости, проходящей через определённую точку в заданное время, рассматривается как объем потока или расход. Объем потока обычно выражается литрами в минуту (л/мин) и связан с относительным давлением жидкости. Например, 10 литров в минуту при 2,7 атм.

Скорость потока (скорость жидкости) определяется как средняя скорость, при которой жидкость движется мимо заданной точки. Как правило, выражается метрами в секунду (м/с) или метрами в минуту (м/мин). Скорость потока является важным фактором при калибровке гидравлических линий.

Объём и скорость потока жидкости традиционно считаются «родственными» показателями. При одинаковом объёме передачи скорость может меняться в зависимости от сечения прохода

Объем и скорость потока часто рассматриваются одновременно. При прочих равных условиях (при неизменном объеме ввода), скорость потока возрастает по мере уменьшения сечения или размера трубы, и скорость потока снижается по мере увеличения сечения.

Так, замедление скорости потока отмечается в широких частях трубопроводов, а в узких местах, напротив, скорость увеличивается. При этом объем воды, проходящей через каждую из этих контрольных точек, остаётся неизменным.

Принцип Бернулли

Широко известный принцип Бернулли выстраивается на той логике, когда подъем (падение) давления текучей жидкости всегда сопровождается уменьшением (увеличением) скорости. И наоборот, увеличение (уменьшение) скорости жидкости приводит к уменьшению (увеличению) давления.

Этот принцип заложен в основе целого ряда привычных явлений сантехники. В качестве тривиального примера: принцип Бернулли «виновен» в том, что занавес душа «втягивается внутрь», когда пользователь включает воду.

Разность давлений снаружи и внутри вызывает силовое усилие на занавес душа. Этим силовым усилием занавес и втягивается внутрь.

Другим наглядным примером является флакон духов с распылителем, когда нажимом кнопки создаётся область низкого давления за счёт высокой скорости воздуха. А воздух увлекает за собой жидкость.

Принцип Бернулли для самолётного крыла: 1 — низкое давление; 2 — высокое давление; 3 — быстрое обтекание; 4 — медленное обтекание; 5 — крыло

Принцип Бернулли также показывает, почему окна в доме имеют свойства самопроизвольно разбиваться при ураганах. В таких случаях крайне высокая скорость воздуха за окном приводит к тому, что давление снаружи становится намного меньше давления внутри, где воздух остаётся практически без движения.

Существенная разница в силе попросту выталкивает окна наружу, что приводит к разрушению стекла. Поэтому когда приближается сильный ураган, по сути, следует открыть окна как можно шире, чтобы уравнять давление внутри и снаружи здания.

И ещё парочка примеров, когда действует принцип Бернулли: подъем самолёта с последующим полётом за счёт крыльев и движение «кривых шаров» в бейсболе.

В обоих случаях создаётся разница скорости проходящего воздуха мимо объекта сверху и снизу. Для крыльев самолета разница скорости создаётся движением закрылков, в бейсболе — наличием волнистой кромки.

Практика домашнего сантехника

Гидростатическое давление: формула и свойства.

Содержание

Гидростатикой называется раздел гидравлики, в котором изучаются законы равновесия жидкостей и рассматривается практическое приложение этих законов. Для того, чтобы понять гидростатику необходимо определиться в некоторых понятиях и определениях.

Закон Паскаля для гидростатики.

В 1653 году французским ученым Б. Паскалем был открыт закон, который принято называть основным законом гидростатики.

Давление на поверхность жидкости, произведенное внешними силами, передается в жидкости одинаково во всех направлениях.

Закон Паскаля легко понимается если взглянуть на молекулярное строение вещества. В жидкостях и газах молекулы обладают относительной свободой, они способны перемещаться друг относительно друга, в отличии от твердых тел. В твердых телах молекулы собраны в кристаллические решетки.

Относительная свобода, которой обладают молекулы жидкостей и газов, позволяет передавать давление производимое на жидкость или газ не только в направлении действия силы, но и во всех других направлениях.

Закон Паскаля для гидростатики нашел широкое распространение в промышленности. На этом законе основана работа гидроавтоматики, управляющей станками с ЧПУ, автомобилями и самолетами и многих других гидравлических машин.

Определение и формула гидростатического давления

Из описанного выше закона Паскаля вытекает, что:

Гидростатическое давление – это давление, производимое на жидкость силой тяжести.

Величина гидростатического давления не зависит от формы сосуда, в котором находится жидкость и определяется произведением

ρ – плотность жидкости

g – ускорение свободного падения

h – глубина, на которой определяется давление.

Для иллюстрации этой формулы посмотрим на 3 сосуда разной формы.

Во всех трёх случаях давление жидкости на дно сосуда одинаково.

Полное давление жидкости в сосуде равно

P0 – давление на поверхности жидкости. В большинстве случаев принимается равным атмосферному.

Сила гидростатического давления

Выделим в жидкости, находящейся в равновесии, некоторый объем, затем рассечем его произвольной плоскостью АВ на две части и мысленно отбросим одну из этих частей, например верхнюю. При этом мы должны приложить к плоскости АВ силы, действие которых будет эквивалентно действию отброшенной верхней части объема на оставшуюся нижнюю его часть.

Рассмотрим в плоскости сечения АВ замкнутый контур площадью ΔF, включающий в себя некоторую произвольную точку a. Пусть на эту площадь воздействует сила ΔP.

Тогда гидростатическое давление формула которого выглядит как

представлет собой силу, действующую на единицу площади, будет называться средним гидростатическим давлением или средним напряжением гидростатического давления по площади ΔF.

Истинное давление в разных точках этой площади может быть разным: в одних точках оно может быть больше, в других – меньше среднего гидростатического давления. Очевидно, что в общем случае среднее давление Рср будет тем меньше отличаться от истинного давления в точке а, чем меньше будет площадь ΔF, и в пределе среднее давление совпадет с истинным давлением в точке а.

Для жидкостей, находящихся в равновесии, гидростатическое давление жидкости аналогично напряжению сжатия в твердых телах.

Единицей измерения давления в системе СИ является ньютон на квадратный метр (Н/м 2 ) – её называют паскалем (Па). Поскольку величина паскаля очень мала, часто применяют укрупненные единицы:

килоньютон на квадратный метр – 1кН/м 2 = 1*10 3 Н/м 2

меганьютон на квадратный метр – 1МН/м 2 = 1*10 6 Н/м 2

Давление равное 1*10 5 Н/м 2 называется баром (бар).

В физической системе единицей намерения давления является дина на квадратный сантиметр (дина/м 2 ), в технической системе – килограмм-сила на квадратный метр (кгс/м 2 ). Практически давление жидкости обычно измеряют в кгс/см 2 , а давление равное 1 кгс/см 2 называется технической атмосферой (ат).

Между всеми этими единицами существует следующее соотношение:

1ат = 1 кгс/см 2 = 0,98 бар = 0,98 * 10 5 Па = 0,98 * 10 6 дин = 10 4 кгс/м 2

Следует помнить что между технической атмосферой (ат) и атмосферой физической (Ат) существует разница. 1 Ат = 1,033 кгс/см 2 и представляет собой нормальное давление на уровне моря. Атмосферное давление зависит от высоты расположения места над уровнем моря.

Измерение гидростатического давления

На практике применяют различные способы учета величины гидростатического давления. Если при определении гидростатического давления принимается во внимание и атмосферное давление, действующее на свободную поверхность жидкости, его называют полным или абсолютным. В этом случае величина давления обычно измеряется в технических атмосферах, называемых абсолютными (ата).

Часто при учете давления атмосферное давление на свободной поверхности не принимают во внимание, определяя так называемое избыточное гидростатическое давление, или манометрическое давление, т.е. давление сверх атмосферного.

Манометрическое давление определяют как разность между абсолютным давлением в жидкости и давлением атмосферным.

Рман = Рабс – Ратм

и измеряют также в технических атмосферах, называемых в этом случае избыточными.

Случается, что гидростатическое давление в жидкости оказывается меньше атмосферного. В этом случае говорят, что в жидкости имеется вакуум. Величина вакуума равняется разнице между атмосферным и и абсолютным давлением в жидкости

Рвак = Ратм – Рабс

и измеряется в пределах от нуля до атмосферы.

Свойства гидростатического давления

Гидростатическое давление воды обладает двумя основными свойствами:
Оно направлено по внутренней нормали к площади, на которую действует;
Величина давления в данной точке не зависит от направления (т.е. от ориентированности в пространстве площадки, на которой находится точка).

Первое свойство является простым следствием того положения, что в покоящейся жидкости отсутствуют касательные и растягивающие усилия.

Предположим, что гидростатическое давление направлено не по нормали, т.е. не перпендикулярно, а под некоторым углом к площадке. Тогда его можно разложить на две составляющие – нормальную и касательную. Наличие касательной составляющей из-за отсутствия в покоящейся жидкости сил сопротивления сдвигающим усилиям неизбежно привело бы к движению жидкости вдоль площадки, т.е. нарушило бы её равновесие.

Поэтому единственным возможным направлением гидростатического давления является его направление по нормали к площадке.

Если предположить что гидростатическое давление направлено не по внутренней, а по внешней нормали, т.е. не внутрь рассматриваемого объекта а наружу от него, то вследствие того, что жидкость не оказывает сопротивления растягивающим усилиям – частицы жидкости пришли бы в движение и её равновесие было бы нарушено.

Следовательно, гидростатическое давление воды всегда направлено по внутренней нормали и представляет собой сжимающее давление.

Из этого же правило следует, что если измениться давление в какой-то точке, то на такую же величину измениться давление в любой другой точке этой жидкости. В этом заключается закон Паскаля, который формулируется следующим образом: Давление производимое на жидкость, передается внутри жидкости во все стороны с одинаковой силой.

На применение этого закона основываются действие машин, работающих под гидростатическим давлением.

Ещё одним фактором влияющим на величину давления является вязкость жидкости, которой до недавнего времени приято было пренебрегать. С появлением агрегатов работающих на высоком давлении вязкость пришлось так же учитывать. Оказалось, что при изменении давления, вязкость некоторых жидкостей, таких как масла, может изменяться в несколько раз. А это уже определяет возможность использовать такие жидкости в качестве рабочей среды.