Как найти температурный коэффициент давления

Коэффициент давления

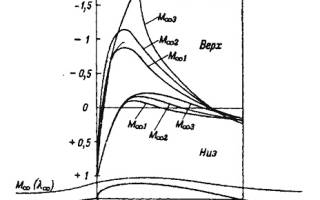
Поместим в газовой поток дозвуковой скорости некоторый криволинейный профиль и рассмотрим изменение параметров элементарной струйки, охватывающей такой профиль (рис. 10.1).

Рисунок 10.1 — Распределение коэффициентов давления по профилю

Создаваемые профилем возмущения потока при дозвуковых скоростях будут распространяться во всех направлениях, в том числе и против течения. Под влиянием этих возмущений элементарные струйки, движущиеся к профилю, будут деформироваться. У носика профиля центральная струйка расширяется; скорость течения при этом падает и в точке разветвления А обращается в нуль. В этой точке параметры будут равны параметрам полного торможения потока. На передней части профиля сечение струйки уменьшается, вследствие чего скорость увеличивается, а давление падает. На верхней и нижней поверхностях профиля продолжается поджатие струйки с соответствующим нарастанием скорости. В некоторой точке сечение струйки минимально. В этом месте скорость будет максимальной. Далее, на задних поверхностях профиля струйка вновь расширяется, скорость ее падает, а давление растет.

Таким образом, в результате деформации струек, характер которой определяется формой обтекаемого тела, вдоль поверхности профиля давление меняется. Распределение давлений обусловливает возникновение аэродинамических сил, действующих на профиль: подъемной силы, вызванной разностью давлений на верхней и нижней поверхностях профиля, и силы лобового сопротивления, вызванной разностью давлений на переднюю и заднюю части профиля и силами трения.

Распределение давлений вдоль обтекаемой поверхности характеризуется безразмерной величиной — коэффициентом давления, который определяется как отношение разности давлений в данной точке на поверхности и статического в бесконечности к скоростному напору невозмущенного потока:

. (10.9)

Коэффициент давления можно определить и по следующей формуле:

, (10.10)

где — число Маха:

, (10.11)

где — скорость потока;

— местная скорость звука.

,

так как (9.17), то получим: и используя (10.11), получим:

.

Число Маха является критерием подобия в механике жидкости и газа и представляет собой отношение скорости течения в данной точке газового потока к местной скорости распространения звука в движущейся среде. Назван по имени австрийского ученого Эрнста Маха.

Если в рассматриваемой области скорости меньше критической, т. е. если:

, то . (10.12)

Если скорости течения больше критической:

, то , (10.13)

где — критическая скорость, то есть скорость течения равная местной скорости звука [см. прим.];

— максимальной скорость течения. (Если применить уравнение энергии к двум сечениям трубки тока, в одном из которых давление уменьшается до нуля, то скорость течения будет стремиться к некоторой максимальной величине , которая удовлетворяет истечению газа в пустоту ( ; ; ). При максимальной скорости течения вся тепловая энергия молекул преобразуется в энергию направленного движения. Практически максимальная скорость течения недостижима и является известным теоретическим пределом для скорости газа. Следует иметь в виду, что с приближением скорости течения к максимальной разрежение газа становится весьма большим и поэтому к рассматриваемому потоку нельзя применять уравнение энергии в известной нам форме (9.7)).

В первом случае (10.12) течение называется дозвуковым или докритическим; а во втором (10.13) — сверхзвуковым или сверхкритическим. Следовательно, значение безразмерной скорости разделяет области течений с дозвуковыми (докритическими) скоростями и со сверхзвуковыми (сверхкритическими) скоростями.

При малых скоростях набегающего потока более удобно для подсчета коэффициента давления пользоваться формулой (10.9).

10.3 Критическое число

На рис. 10.1 показано примерное распределение вдоль поверхности профиля. До тех пор, пока скорость значительно меньше скорости звука, характер деформации струек, а вместе с тем и картина распределения коэффициентов давления по профилю при изменении скорости невозмущенного потока сохраняются практически неизменными. Однако по мере увеличения влияние сжимаемости сказывается все более ощутимо; распределение по профилю начинает меняться особенно сильно там, где местные скорости в струйке (на поверхности профиля) велики. В минимальном сечении струйки скорость наибольшая. Найдем зависимость между безразмерной скоростью и скоростью в некоторой точке на профиле .

С этой целью воспользуемся формулой (10.10), заменив в ней отношение давлений через соответствующие числа М, с учетом, что:

и

, (10.14)

где — формула отношения давлений в предположении изоэнтропического течения, являющаяся модификацией уравнения энергии, полученного путем преобразования уравнения (9.7) и введения безразмерной скорости .

При некотором значении , которое обозначим через в минимальном сечении трубки тока устанавливается критическая скорость . Соответствующая величина коэффициента давления будет равна:

, (10.15)

Величина , называется критическим числом набегающего потока. Оно определяет то значение безразмерной скорости набегающего потока, при котором максимальная местная скорость на контуре тела становится равной местной скорости звука.

Из определения критического числа (см. выше), следует, что эта величина разграничивает дозвуковые режимы обтекания тела на две группы. Первая группа докритических режимов ( ) характеризуется тем, что во всех точках поля потока местные скорости дозвуковые ( ). Ко второй группе ( ) относятся режимы обтекания с местными сверхзвуковыми скоростями.

Примечание: [При дозвуковом обтекании фюзеляжа, крыла и оперения самолёта на выпуклых участках их обводов возникают зоны местного ускорения потока. Когда скорость полёта летательного аппарата приближается к звуковой, местная скорость движения воздуха в зонах ускорения потока может несколько превысить скорость звука (рис. 10.2). Миновав зону ускорения, поток замедляется, с неизбежным образованием ударной волны (таково свойство сверхзвуковых течений: переход от сверхзвуковой скорости к дозвуковой всегда происходит разрывно — с образованием ударной волны). Интенсивность этих ударных волн невелика — перепад давления на их фронтах мал, но они возникают сразу во множестве, в разных точках поверхности аппарата, и в совокупности они резко меняют характер его обтекания, с ухудшением его лётных характеристик: подъёмная сила крыла падает, воздушные рули и элероны теряют эффективность, аппарат становится неуправляемым, и всё это носит крайне нестабильный характер, возникает сильная вибрация. Это явление получило название волнового кризиса. Когда скорость движения аппарата становится сверхзвуковой (М > 1), течение вновь становится стабильным, хотя его характер изменяется принципиально (рис. 10.3).]

Рисунок 10.2 — Аэрокрыло в близком к звуковому потоке

Рисунок 10.3 — Аэрокрыло в сверхзвуковом потоке

Большая Энциклопедия Нефти и Газа

Температурный коэффициент — давление

Температурный коэффициент давления — ф ( С) 1 для рабочих жидкостей при постоянном начальном давлении р величина почти постоянная, что позволяет иметь у жидкостных термометров равномерную шкалу. [1]

Температурный коэффициент давления водорода , равный ] / 27 t его давления при 0, считается строго постоянным по самому определению понятия о нормальной температурной шкале. [2]

Температурный коэффициент давления насыщенного пара достаточно велик, вследствие чего конденсационные термометры обладают высокой чувствительностью. [4]

Если величина температурного коэффициента давления ( dt [ dp) определена экспериментально, то значения температур кипения можно привести к 760 мм с помощью этой величины без формулы Крафтса. [5]

Что называется температурным коэффициентом давления . Какой процесс был использован в работе. [6]

Величину а называют температурным коэффициентом давления . [7]

Величина — называется температурным коэффициентом давления насыщенного пара вещества . [8]

Из (6.17) видно, что температурный коэффициент давления газа равен относительному изменению давления газа, происходящему при его нагревании на 1 С. [9]

Формула, полученная для вычисления температурного коэффициента давления газа , является неточной, так как при ее выводе не были учтены такие факторы, как расширение стенок стеклянной трубки барометра, изменение длины столбов ртути в барометре и манометре от нагревания. [10]

Зависимость давления насыщения от температуры характеризуется температурным коэффициентом давления насыщения , который определяется составом пластовой нефти. По данным [25], для нефти Ромашкинского месторождения этот коэффициент равен 0 01 — 0 02 МПа / С, а для нефти Ново-Дмитриевского месторождения этот показатель составляет 0 06 ч — 0 08 МПа / С. [11]

Приближенно теплота диссоциации может быть вычислена из температурного коэффициента давления диссоциации гидрата . Для сравнения выгодно проводить его измерение приблизительно в тех же условиях, что и определение энергии активации. [12]

Следует, однако, иметь в виду, что температурный коэффициент давления газа , полученный при измерении температуры по ртутному термометру, не в точности одинаков для разных температур: закон Шарля выполняется только приближенно, хотя и с очень большой степенью точности. [13]

Следует иметь, однако, в виду, что температурный коэффициент давления газа , полученный при измерении температуры по ртутному термометру, не в точности одинаков для разных температур: закон Шарля выполняется только приближенно, хотя и с очень большой степенью точности. [14]

Как видно из формулы ( 3), определение температурного коэффициента давления газа сводится к определению двух давлений pi и рг и соответствующих им температур ti и U при постоянном объеме. Для определения температурного коэффициента давления газа может быть использован газовый термометр. [15]

коэффициент давления

коэффицие́нт давле́ния в аэродинамике — безразмерная величина c_p, равная разности местного давления p я давления в невозмущённом потоке p_∞ отнесённой к скоростному напору невозмущённого потока:

,

где ρ_∞, V_∞ — плотность и скорость газа невозмущённого потока (на бесконечности).

Энциклопедия «Авиация». — М.: Большая Российская Энциклопедия . Свищёв Г. Г. . 1998 .

Смотреть что такое «коэффициент давления» в других словарях:

коэффициент давления — (cp) Безразмерная величина, равная разности местного давления и давления в невозмущенном потоке, отнесенной к скоростному напору невозмущенного потока . [ГОСТ 23281 78] Тематики аэродинамика летательных аппаратов Обобщающие термины характеристики … Справочник технического переводчика

коэффициент давления — slėgio koeficientas statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, skaitine verte lygus slėgio pokyčiui, kai temperatūra pakinta 1 K, t. y. β = dp/dT; čia dp – slėgio pokytis, dT – temperatūros pokytis. atitikmenys: angl.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

коэффициент давления — slėgio koeficientas statusas T sritis fizika atitikmenys: angl. pressure coefficient vok. Druckkoeffizient, m rus. коэффициент давления, m pranc. coefficient de pression, m … Fizikos terminų žodynas

коэффициент давления — в аэродинамике — безразмерная величина cp, равная разности местного давления p я давления в невозмущённом потоке p∞ отнесённой к скоростному напору невозмущённого потока: ,где ρ∞, V∞ — плотность и скорость газа невозмущённого потока (на … Энциклопедия «Авиация»

Коэффициент давления в аэродинамике — безразмерная величина cp, равная разности местного давления p я давления в невозмущённом потоке р∞ отнесённой к скоростному напору невозмущённого потока. Авиация: Энциклопедия. М.: Большая Российская Энциклопедия. Главный редактор Г.П. Свищев.… … Энциклопедия техники

температурный коэффициент давления — temperatūrinis slėgio koeficientas statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. relative pressure coefficient vok. Spannungskoeffizient, m rus. температурный… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

термический коэффициент давления — temperatūrinis slėgio koeficientas statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. relative pressure coefficient vok. Spannungskoeffizient, m rus. температурный… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

температурный коэффициент давления — temperatūrinis slėgio koeficientas statusas T sritis fizika atitikmenys: angl. relative pressure coefficient vok. Spannungskoeffizient, m rus. температурный коэффициент давления, m; термический коэффициент давления, m pranc. coefficient… … Fizikos terminų žodynas

термический коэффициент давления — temperatūrinis slėgio koeficientas statusas T sritis fizika atitikmenys: angl. relative pressure coefficient vok. Spannungskoeffizient, m rus. температурный коэффициент давления, m; термический коэффициент давления, m pranc. coefficient… … Fizikos terminų žodynas

Термитаский коэффициент давления насыщения нефти газом. — 5. Термитаский коэффициент давления насыщения нефти газом. Приращение величины давления насыщения при изменении температуры нефти на один градус. Источник … Словарь-справочник терминов нормативно-технической документации

Определение термического коэффициента давления газа

Страницы работы

Содержание работы

Министерство путей сообщения

государственный университет путей сообщения

Лабораторная работа 104

Коэффициента давления газа

Если объем некоторой массы газа поддерживать постоянным, то давление от температуры будет зависеть линейно.

где – давление газа при 0°С,

– давление газа при t°С,

– термический коэффициент давления газа.

Термический коэффициент давления показывает, на какую часть увеличивается первоначальное давление газа, находящегося при 0°С при нагревании на 1°С в постоянном объеме.

Для реальных газов термический коэффициент давления – величина, зависящая от давления и температуры. Зная два значения давления, соответствующее двум различным значениям температур можно найти средний термический коэффициент давления каза для этого интервала температур.

Цель работы: определить термический коэффициент давления воздуха.

Если тогда

из графика . Значит .

Определение термического коэффициента давления газа, температуры абсолютного нуля и подтверждение газового закона Шарля

· С помощью нагрева замкнутого объема газа до Т=100С изучить линейность зависимости давления газа от его температуры

· На основании этой зависимости найти температурный коэффициент давления газа

· Экспериментальная определить температуру абсолютного нуля Т0

Оборудование и материалы:

Лабораторный комплекс ЛКТ-9 (см. Приложение 2), включающий чайник, герметичный сосуд, манометр, шланги, кран, штуцер

Все газы при давлениях Р, не превышающих существенно атмосферное давление Р_атм=10 5 н/м 2 =10 5 Па (Р

Р-давление газа, V-его объем,

Т-его температура по шкале Кельвина ( получается прибавлением к температуре по шкале Цельсия 273 градуса)

Из этого закона получаются все остальные газовые законы

· Закон Бойля—Мариотта (m = const, T = const).

· Закон Гей-Люссака (m = const, P = const)

· Закон Шарля (m = const, V = const).

Для данной массы газа при постоянном объеме давление газа изменяется линейно с ростом температуры:
,
где P – давление газа при температуре t°;
P – давление газа при 0°C;
g – термический коэффициент давления газа ( ).

Термический коэффициент давления газа показывает, на какую часть относительно первоначального давления изменится давление газа при его нагревании на 1°С.

Для идеального газа также .

Изохорический процесс, т.е. процесс, протекающий при постоянном объеме на диаграмме (P, t°) изобразится прямой линией. Различные прямые соответствую различным объемам и называются изохорами.

Заметим теперь, что все изобары и изохоры пересекают ось t° в одной и той же точке, определяемой из условия 1+γ×t°=0. Откуда .

Если за начало отсчета температуры взять нуль (как это и было), то получим шкалу температур по Цельсию. Если сместить начало отсчета в точку -273.15, то перейдем к другой температурной шкале, которая называется абсолютной (или шкалой Кельвина).

В соответствии с определением абсолютной шкалы между абсолютной температурой (Т) и температурой по Цельсию (t) существует следующее соотношение:

. (1)

Температура, равная 0°К называется абсолютным нулем.

Для установления абсолютной шкалы температур и абсолютного нуля мы воспользовались законами Гей-Люссака и Шарля и поступили сугубо формально. Однако Кельвин в 1852г., исходя из иных физических соображений установил такую же абсолютную шкалу температур с тем же значением абсолютного нуля, какие ранее были получены формально. Поэтому понятия абсолютной температуры и абсолютного нуля не следует рассматривать как формальные, не имеющие физического смысла. Кельвин показал, что абсолютный нуль – это самая низкая из возможных температур вещества. При абсолютном нуле прекращается хаотическое движение молекул в веществе. Однако это не означает, что в нем прекращается всякое движение. Сохраняется, например, движение электронов в атоме. В настоящее время удается охлаждать малые объемы вещества до температуры очень близкой к абсолютному нулю, не достигая последнего лишь на несколько тысячных долей градуса.

Перейдем теперь в уравнении, описывающего закон Шарля от температуры по Цельсию к абсолютной температуре, подставив вместо t величину .

Тогда

Из этого следует, что

где индексы 1 и 2 относятся к произвольным состояниям, лежащим на одной и той же изобаре (для уравнения (9.3)), или одной и той же изохоре (для уравнения (9.4)).

Итак, при постоянном давлении объем газа пропорционален абсолютной температуре; и при постоянном объеме давление газа пропорционально абсолютной температуре.

Всякий реальный газ тем точнее следует уравнениям PV = const, , , чем меньше его плотность, т.е., чем больший объем он занимает.

В соответствии с уравнением PV = const, объем растет с уменьшением давления, а согласно с объем возрастает с температурой. Следовательно, рассмотренные газовые законы справедливы при не слишком низких температурах и невысоких давлениях.

Газ, который точно следует этим уравнениям, называется идеальным. Всякий реальный газ по мере убывания его плотности приближается к идеальному.

studopedia.org — Студопедия.Орг — 2014-2019 год. Студопедия не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования (0.003 с) .