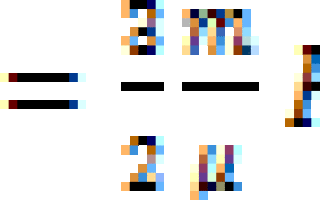В изобарном процессе давление

Изобарный процесс. При изобарном процессе передаваемое газу количеству теплоты идет на изменение его внутренней энергии и на совершение работы при постоянном давлении (p=const)

При изобарном процессе передаваемое газу количеству теплоты идет на изменение его внутренней энергии и на совершение работы при постоянном давлении (p=const). Q=U+A

24. Термодинамическая шкала температур. Абсолютный нуль.

Из повседневного опыта известно, что тела бывают горячими и холодными, то есть по разному нагретыми. Для количественного описания такого различия, то есть для описания степени нагретости в физике ввели понятие температуры. При соприкосновении по разному нагретых тел более холодное начинает нагреваться, а более горячее – охлаждаться. Такой процесс называют теплопередачей (обмен тепла). В этом процессе температуры тел становятся одинаковыми. В конце концов наступает момент, когда все соприкасающиеся тела имеют одинаковую температуру. Такое состояние называют тепловым равновесием. В этом состоянии не происходит уже никаких изменений температуры.

Термодинамическое (тепловое) равновесия – состояние, в котором не происходит никаких изменений термодинамических параметров – температуры, давления, плотности и т.д.

Температура – физический параметр, одинаковый во всех частях системы тел, находящихся в состоянии теплового равновесия.

Для измерения температуры используются различные шкалы температур.

В качестве нуля температурной шкалы – 0 0 С- выбрана точка плавления льда, а точке кипения воды приписано значение в 100 0 С. В качестве единицы измерения – градус Цельсия – принята 1/100 часть интервала между этими точками.

Шкала Кельвина (абсолютная шкала температур):

В качестве нуля принят так называемый абсолютный ноль температуры, то есть температура ниже которой невозможно ничего охладить. Единица измерения – градус Кельвина- выбран равным градусу Цельсия. Так как точка таяния льда имеет температуру 273,15 К, то связь между шкалой Цельсия и шкалой Кельвина следующая:

Т (К) = Т ( 0 С) = +273,15

Абсолютный ноль температуры также невозможно достичь, как и отрицательные температуры. Это утверждение представляет собой –третий закон термодинамики. В МКТ температура характеризует величину средней энергии хаотичного движения молекул – у более теплого тела молекулы движутся быстрее.

25. Первое начало термодинамики (первый закон термодинамики).

Энергия, полученная системой путем теплообмена, расходуется на изменение ее внутренней энергии и на работу против внешних сил.

Первое начало термодинамики:

Тепло, переданное газу, расходуется на – изменение его внутренней энергии (нагрев), совершение газом работы (например, при его расширении).

Изменение внутренней энергии системы равно сумме работы внешних сил и количеству теплоты, переданного системе:

26. Внутренняя энергия идеального газа ( одноатомного, двух атомного, много атомного).

(Одноатомный газ)

(двухатомный газ)

(многоатомный газ)

Где — кол – во вещества, -газовая постоянная (8,31 Дж/моль), Т – термодинамическая постаянная.

27. Вывод уравнения объединенного газового закона

Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа.

Уравнение Клапейрона-Менделеева показывает, что для данной массы газа возможно одновременно изменение трех параметров, характеризующих состояние идеального газа.

R, где R — универсальная газовая постоянная , R = 8,31 Дж/моль. P-давление(паскаль), V-объем(м 3 ), T-термодинамическая температура (к), – количество вещества υ . дописать

93.79.221.197 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Изобарный процесс, связанные с ним уравнения и вывод формулы работы

Изобарный процесс (также называемый изобарическим процессом) является одним из термодинамических процессов, которые происходят при постоянном показателе давления. Масса газа системы при этом также остается постоянной. Наглядное представление о графике, демонстрирующем изобарный процесс, дает термодинамическая диаграмма в соответствующей системе координат.

Наиболее простым примером изобарического процесса можно назвать нагревание некоторого объема воды в открытом сосуде. В качестве еще одного примера можно привести расширение идеального газа в цилиндрическом объеме, где поршень имеет свободный ход. В каждом из этих случаев давление будет постоянным. Оно равно обыкновенному атмосферному давлению, что вполне очевидно.

Обратимость

Изобарный процесс можно считать обратимым в том случае, если давление в системе совпадает с внешним давлением и равно во все моменты времени процесса (то есть оно постоянно по своему значению), а температура изменяется очень медленно. Таким образом, термодинамическое равновесие в системе сохраняется в каждый момент времени. Именно совокупность вышеперечисленных факторов дает нам возможность считать изобарный процесс обратимым.

Чтобы осуществить в системе изобарический процесс, теплоту к ней нужно или подводить, или отводить. При этом теплота должна расходоваться на работу расширения идеального газа и на изменение его внутренней энергии. Формулу, демонстрирующую зависимость величин друг от друга при изобарном процессе, называют законом Гей-Люссака. Она показывает, что объем пропорционален температуре. Давайте выведем эту формулу на основании поверхностных знаний.

Вывод закона Гей-Люссака (первичное понимание)

Человек, хотя бы немного разбирающийся в молекулярной физике, знает, что многие задачи связаны с определенными параметрами. Имя им – давление газа, объем газа и температура газа. В тех или иных случаях в ход идут молекулярная и молярная масса, количество вещества, универсальная газовая постоянная и другие показатели. И здесь есть определенная связь. Давайте поговорим об универсальной газовой постоянной подробнее. На тот случай, если кто-то не знает, каким образом ее получили.

Получение универсальной газовой постоянной

Эту константу (постоянное число с определенной размерностью) принято также называть постоянной Менделеева. Она присутствует также в уравнении Менделеева-Клапейрона для идеального газа. Как же получил наш знаменитый физик эту константу?

Как мы знаем, уравнение идеального газа имеет следующую форму: PV/T (что озвучивается так: “произведение давления на объем, деленное на температуру”). По отношению к универсальной газовой постоянной применим так называемый закон Авогадро. Он гласит о том, что если мы возьмем любой газ, то одинаковое его количество молей при одинаковой температуре и одинаковом давлении займет одинаковый объем.

По сути дела, это есть словесная формулировка уравнения состояния идеального газа, которое было записано в виде формулы немного ранее. Если мы возьмем нормальные условия (а это когда температура газа равна 273,15 Кельвинов, давление равно 1 атмосфере, соответственно, 101325 Паскалей, а объем моля газа равен 22,4 литра) и подставим их в уравнение, все перемножим и разделим, то получим, что совокупность подобных действий дает нам численный показатель, равный 8,31. Размерность дается в Джоулях, деленных на произведение моля на Кельвин (Дж/моль*К).

Уравнение Менделеева-Клапейрона

Давайте возьмем уравнение состояния идеального газа и перепишем его в новом виде. Изначальное уравнение, напомним, имеет вид PV/T=R. А теперь умножим обе части на температурный показатель. Получим формулу PV(м)=RT. То есть произведение давления на объем равно произведению универсальной газовой постоянной на температуру.

Теперь умножим обе части уравнения на то или иное количество молей. Обозначим их количество буквой, скажем, X. Таким образом, получим следующую формулу: PV(м)X=XRT. Но ведь мы знаем, что произведение V с индексом “м” дает нам в результате просто объем V, а число молей X раскрывается в виде деления частной массы на молярную массу, то есть имеет вид m/M.

Таким образом, конечная формула будет выглядеть следующим образом: PV=MRT/m. Это и есть то самое уравнение Менделеева-Клапейрона, к которому пришли оба физика практически одновременно. Мы можем умножить правую часть уравнения (и в то же время разделить) на число Авогадро. Тогда получим: PV = XN(a)RT/N(a). Но ведь произведение количества молей на число Авогадро, то есть XN(a), дает нам не что иное, как общее число молекул газа, обозначаемое буквой N.

В то же время частное от универсальной газовой постоянной и числа Авогадро – R/N(a) даст постоянную Больцмана (обозначается k). В итоге мы получим еще одну формулу, но уже в несколько другом виде. Вот она: PV=NkT. Можно раскрыть эту формулу и получить следующий результат: NkT/V=P.

Работа газа при изобарном процессе

Как мы выяснили ранее, изобарным процессом называется термодинамический процесс, при котором давление остается величиной постоянной. А чтобы выяснить, как будет определяться работа при изобарном процессе, нам придется обратиться к первому началу термодинамики. Общая формула выглядит следующим образом: dQ = dU + dA, где dQ — это количество теплоты, dU – изменение внутренней энергии, а dA – работа, совершаемая в ходе выполнения термодинамического процесса.

Теперь рассмотрим конкретно изобарный процесс. Примем во внимание тот фактор, что давление остается постоянным. Теперь попытаемся переписать первое начало термодинамики для изобарного процесса: dQ = dU + pdV. Чтобы получить наглядное представление о процессе и работе, нужно изобразить его в системе координат. Ось абсцисс обозначим p, ось ординат V. Пускай объем будет увеличиваться. В двух отличных друг от друга точках с соответствующим значением p (конечно же, фиксированным) отметим состояния, представляющие собой V1 (первоначальный объем) и V2 (конечный объем). В этом случае график будет представлять собой прямую линию, параллельную оси абсцисс.

Найти работы в таком случае проще простого. Это будет просто площадь фигуры, ограниченная с двух сторон проекциями на ось абсцисс, а с третьей стороны – прямой линией, соединяющей точки, лежащие, соответственно, в начале и конце изобарной прямой. Попробуем вычислить значение работы при помощи интеграла.

Он будет вычисляться следующим образом: A = p (интеграл в пределах от V1 до V2) dV. Раскроем интеграл. Получим, что работа будет равна произведению давления на разность объемов. То есть выглядеть формула будет следующим образом: A = p (V2 – V1). Если мы раскроем некоторые величины, то получим еще одну формулу. Она выглядит так: A = xR (T2 – T2), где x – количество вещества.

Универсальная газовая постоянная и ее смысл

Можно сказать, что последнее выражение будет определять физический смысл R – универсальной газовой постоянной. Чтобы было понятнее, давайте обратимся к конкретным числам. Возьмем для проверки один моль какого-либо вещества. В то же время пускай температурная разница будет составлять 1 Кельвин. В этом случае легко заметить, что работа газа будет равна универсальной газовой постоянной (или же наоборот).

Заключение

Этот факт можно подать немного в другом свете, перефразировав формулировку. Например, универсальная газовая постоянная будет численно равна работе, совершаемой при изобарном расширении одним молем идеального газа, если он нагревается на один Кельвин. Вычислить работу при других изопроцессах будет несколько сложнее, но главное — при этом применять логику. Тогда все быстро встанет на свои места, и вывод формулы окажется проще, чем вы думаете.

Изопроцессы

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: изопроцессы — изотермический, изохорный, изобарный процессы.

На протяжении этого листка мы будем придерживаться следующего предположения: масса и химический состав газа остаются неизменными. Иными словами, мы считаем, что:

• , то есть нет утечки газа из сосуда или, наоборот, притока газа в сосуд;

• , то есть частицы газа не испытывают каких-либо изменений (скажем, отсутствует диссоциация — распад молекул на атомы).

Эти два условия выполняются в очень многих физически интересных ситуациях (например, в простых моделях тепловых двигателей) и потому вполне заслуживают отдельного рассмотрения.

Если масса газа и его молярная масса фиксированы, то состояние газа определяется тремя макроскопическими параметрами: давлением, объёмом и температурой. Эти параметры связаны друг с другом уравнением состояния (уравнением Менделеева — Клапейрона).

Термодинамический процесс (или просто процесс) — это изменение состояния газа с течением времени. В ходе термодинамического процесса меняются значения макроскопических параметров — давления, объёма и температуры.

Особый интерес представляют изопроцессы — термодинамические процессы, в которых значение одного из макроскопических параметров остаётся неизменным. Поочерёдно фиксируя каждый из трёх параметров, мы получим три вида изопроцессов.

1. Изотермический процесс идёт при постоянной температуре газа: .
2. Изобарный процесс идёт при постоянном давлении газа: .
3. Изохорный процесс идёт при постоянном объёме газа: .

Изопроцессы описываются очень простыми законами Бойля — Мариотта, Гей-Люссака и Шарля. Давайте перейдём к их изучению.

Изотермический процесс

Пусть идеальный газ совершает изотермический процесс при температуре . В ходе процесса меняются только давление газа и его объём.

Рассмотрим два произвольных состояния газа: в одном из них значения макроскопических параметров равны , а во втором — . Эти значения связаны уравнением Менделеева-Клапейрона:

Как мы сказали с самого начала,масса и молярная масса предполагаются неизменными.

Поэтому правые части выписанных уравнений равны. Следовательно, равны и левые части:

Поскольку два состояния газа были выбраны произвольно, мы можем заключить, что в ходе изотермического процесса произведение давления газа на его объём остаётся постоянным:

Данное утверждение называется законом Бойля — Мариотта.

Записав закон Бойля — Мариотта в виде

можно дать и такую формулировку: в изотермическом процессе давление газа обратно пропорционально его объёму. Если, например, при изотермическом расширении газа его объём увеличивается в три раза, то давление газа при этом в три раза уменьшается.

Как объяснить обратную зависимость давления от объёма с физической точки зрения? При постоянной температуре остаётся неизменной средняя кинетическая энергия молекул газа, то есть, попросту говоря, не меняется сила ударов молекул о стенки сосуда. При увеличении объёма концентрация молекул уменьшается, и соответственно уменьшается число ударов молекул в единицу времени на единицу площади стенки — давление газа падает. Наоборот, при уменьшении объёма концентрация молекул возрастает, их удары сыпятся чаще и давление газа увеличивается.

Графики изотермического процесса

Вообще, графики термодинамических процессов принято изображать в следующих системах координат:

• -диаграмма: ось абсцисс , ось ординат ;
• -диаграмма: ось абсцисс , ось ординат ;
• -диаграмма: ось абсцисс , ось ординат .

График изотермического процесса называется изотермой.

Изотерма на -диаграмме — это график обратно пропорциональной зависимости .

Такой график является гиперболой (вспомните алгебру — график функции ). Изотерма-гипербола изображена на рис. 1 .

Рис. 1. Изотерма на -диаграмме

Каждая изотерма отвечает определённому фиксированному значению температуры. Оказывается, что чем выше температура, тем выше лежит соответствующая изотерма на —диаграмме.

В самом деле, рассмотрим два изотермических процесса, совершаемых одним и тем же газом (рис. 2 ). Первый процесс идёт при температуре , второй — при температуре .

Рис. 2. Чем выше температура, тем выше изотерма

Фиксируем некоторое значение объёма . На первой изотерме ему отвечает давление , на второй — p_1′ class=’tex’ alt=’p_2 > p_1′ /> . Но при фиксированном объёме давление тем больше, чем выше температура (молекулы начинают сильнее бить по стенкам). Значит, T_1′ class=’tex’ alt=’T_2 > T_1′ /> .

В оставшихся двух системах координат изотерма выглядит очень просто: это прямая, перпендикулярная оси (рис. 3 ):

Рис. 3. Изотермы на и -диаграммах

Изобарный процесс

Напомним ещё раз, что изобарный процесс — это процесс, проходящий при постоянном давлении. В ходе изобарного процесса меняются лишь объём газа и его температура.

Типичный пример изобарного процесса: газ находится под массивным поршнем, который может свободно перемещаться. Если масса поршня и поперечное сечение поршня , то давление газа всё время постоянно и равно

где — атмосферное давление.

Пусть идеальный газ совершает изобарный процесс при давлении . Снова рассмотрим два произвольных состояния газа; на этот раз значения макроскопических параметров будут равны и .

Выпишем уравнения состояния:

Поделив их друг на друга, получим:

В принципе, уже и этого могло бы быть достаточно, но мы пойдём немного дальше. Перепишем полученное соотношение так, чтобы в одной части фигурировали только параметры первого состояния, а в другой части — только параметры второго состояния (иными словами, «разнесём индексы» по разным частям):

А отсюда теперь — ввиду произвольности выбора состояний! — получаем закон Гей-Люссака:

Иными словами, при постоянном давлении газа его объём прямо пропорционален температуре:

Почему объём растёт с ростом температуры? При повышении температуры молекулы начинают бить сильнее и приподнимают поршень. При этом концентрация молекул падает, удары становятся реже, так что в итоге давление сохраняет прежнее значение.

Графики изобарного процесса

График изобарного процесса называется изобарой. На -диаграмме изобара является прямой линией (рис. 4 ):

Рис. 4. Изобара на -диаграмме

Пунктирный участок графика означает, что в случае реального газа при достаточно низких температурах модель идеального газа (а вместе с ней и закон Гей-Люссака) перестаёт работать. В самом деле, при снижении температуры частицы газа двигаются всё медленнее, и силы межмолекулярного взаимодействия оказывают всё более существенное влияние на их движение (аналогия: медленный мяч легче поймать, чем быстрый). Ну а при совсем уж низких температурах газы и вовсе превращаются в жидкости.

Разберёмся теперь, как меняется положение изобары при изменении давления. Оказывается, что чем больше давление, тем ниже идёт изобара на —диаграмме.
Чтобы убедиться в этом, рассмотрим две изобары с давлениями и (рис. 5 ):

Рис. 5. Чем ниже изобара, тем больше давление

Зафиксируем некоторое значение температуры . Мы видим, что . Но при фиксированной температуре объём тем меньше, чем больше давление (закон Бойля — Мариотта!).

Стало быть, p_1′ class=’tex’ alt=’p_2 > p_1′ /> .

В оставшихся двух системах координат изобара является прямой линией, перпендикулярной оси (рис. 6 ):

Рис. 6. Изобары на и -диаграммах

Изохорный процесс

Изохорный процесс, напомним, — это процесс, проходящий при постоянном объёме. При изохорном процессе меняются только давление газа и его температура.

Изохорный процесс представить себе очень просто: это процесс, идущий в жёстком сосуде фиксированного объёма (или в цилиндре под поршнем, когда поршень закреплён).

Пусть идеальный газ совершает изохорный процесс в сосуде объёмом . Опять-таки рассмотрим два произвольных состояния газа с параметрами и . Имеем:

Делим эти уравнения друг на друга:

Как и при выводе закона Гей-Люссака, «разносим» индексы в разные части:

Ввиду произвольности выбора состояний мы приходим к закону Шарля:

Иными словами, при постоянном объёме газа его давление прямо пропорционально температуре:

Увеличение давления газа фиксированного объёма при его нагревании — вещь совершенно очевидная с физической точки зрения. Вы сами легко это объясните.

Графики изохорного процесса

График изохорного процесса называется изохорой. На -диаграмме изохора является прямой линией (рис. 7 ):

Рис. 7. Изохора на -диаграмме

Смысл пунктирного участка тот же: неадекватность модели идеального газа при низких температурах.

Далее, чем больше объём, тем ниже идёт изохора на —диаграмме (рис. 8 ):

Рис. 8. Чем ниже изохора, тем больше объём

Доказательство аналогично предыдущему. Фиксируем температуру и видим, что . Но при фиксированной температуре давление тем меньше, чем больше объём (снова закон Бойля — Мариотта). Стало быть, V_1′ class=’tex’ alt=’V_2 > V_1′ /> .

В оставшихся двух системах координат изохора является прямой линией, перпендикулярной оси (рис. 9 ):

Рис. 9. Изохоры на и -диаграммах

Законы Бойля — Мариотта, Гей-Люссака и Шарля называются также газовыми законами.

Мы вывели газовые законы из уравнения Менделеева — Клапейрона. Но исторически всё было наоборот: газовые законы были установлены экспериментально, и намного раньше. Уравнение состояния появилось впоследствии как их обобщение.

Изобарический процесс

Что такое изобарический процесс

Изобарическим (или изобарным) процессом называется процесс, происходящий в неизменной массе газа при постоянном давлении.

Запишем уравнение для двух состояний идеального газа:

[pV_1=nu RT_1left(1right),] [pV_2=nu RT_2 left(2right).]

Разделим уравнение (2) на уравнение (1), получим уравнение изобарного процесса:

Уравнение (4) называют законом Гей-Люссака.

Внутренняя энергия и количество теплоты изобарического процесса

Этот процесс происходит с подводом тепла, если объем увеличивается, или его отводом, чтобы уменьшать объем. Запишем первое начало термодинамики, последовательно получим выражения для работы, внутренней энергии и количества теплоты изобарного процесса:

где $delta Q $- элементарное тепло, подводимое к системе, $dU$- изменение внутренней энергии газа в проводимом процессе, $dA$- элементарная работа, которую совершает газ в процессе, i-число степеней свободы молекулы газа, R — универсальная газовая постоянная, d — количество молей газа.

Попробуй обратиться за помощью к преподавателям

Изменение внутренней энергии газа:

Уравнение (8) определяет работу для изобарного процесса. Вычтем из (2) уравнение (1), получим еще одно уравнение для работы газа в изобарном процессе:

[p<(V>_2-V_1)=nu R<(T>_2-T_1)to A=nu R<(T>_2-T_1) (9)] [triangle Q=frac<2>нR<(T>_2-T_1)+nu R<(T>_2-T_1)=c_nu triangle T (10),]

где $c_$ — молярная теплоёмкость газа при изобарном процессе. Уравнение (10) определяет количество теплоты, сообщаемое газу массы m в изобарном процессе при увеличении температуры на $triangle T.$

Изопроцессы очень часто изображают на термодинамических диаграммах. Так, линия, изображающая на такой диаграмме изобарический процесс, называется изобарой (рис.1).

Задание: Определите, как соотносятся давления $p_1$ и $p_2$ на диаграмме V(T) рис 1с.

Проведем изотерму $T_1$

В точках А и В температуры одинаковы, следовательно, газ подчиняется закону Бойля — Мариотта:

[p_AV_A=p_BV_B (1.2)] [V_A > V_Bto p_A Ответ: Давления $p_1 > p_2$.

Задай вопрос специалистам и получи
ответ уже через 15 минут!

Задание: При неизменном давлении p=3$cdot <10>^5$Па газ расширился от объема $V_1=2л$ до $V_2=4л.$ Найти работу, совершаемую газом.

За основу решения задачи примем формулу работы при расширении газа в изобарном процессе:

Переведем данные объемы в СИ: $V_1=2л=2^<-3>м^3$, $V_2=4л=4<•10>^<-3>м^3$

Ответ: Работа газа в изобарном процессе 600 Дж.

Задание: Сравните работу газа в процессе ABC и работу над газом в процессе CDA рис 3.

За основу решения примем формулу, определяющую работу газа:

Из геометрического смысла определенного интеграла известно, что работа — есть площадь фигуры, которая ограничена функцией подынтегрального выражения, осью абсцисс, и изохорами в точках $V_1 и V_2$ (оси p(V)). Переведем графики процессов в оси p(V).

Рассмотрим каждый отрезок графиков процессов изображенных на рисунке (3).

АВ: Изохорный процесс (p=const), $Vuparrow left( Объем растетright), Tuparrow $;

ВС: Изохорный процесс (V =const), $Tuparrow $ (из графика), p$uparrow $, из закона для изохорного процесса ($frac

=const$);

CD: (p=const), $Vdownarrow , Tdownarrow ;$

DA: (V =const), $Tdownarrow , pdownarrow .$

Изобразим графики процессов в осях p(V) (рис.4):

Работа газа $A_=S_$ ($S_$ — площадь прямоугольника ABFE) (рис. 3). Работа над газом $A_=S_$ ($S_$)$ -площадь прямоугольника $EFCD.Очевидно, что $A_>A_.$

Так и не нашли ответ
на свой вопрос?

Просто напиши с чем тебе
нужна помощь

Изобарический процесс

Изобарный процесс (др.-греч. ισος, isos — «одинаковый» + βαρος, baros — «вес») — термодинамический процесс, происходящий в системе при постоянном внешнем давлении; на термодинамической диаграмме изображается изобарой.

Пример изобарного процесса — расширение газа в цилиндре со свободно ходящим нагруженным поршнем. Если изобарный процесс происходит настолько медленно, что давление в системе можно считать постоянным и равным внешнему давлению, а температуpa меняется так медленно, что в каждый момент времени сохраняется термодинамическое равновесие, то изобарный процесс считается обратимым. Для осуществления

изобарного процесса к системе надо подводить (или отводить) теплоту ΔQ , которая расходуется на работу расширения PdV и изменение внутренней энергии dU, то есть ΔQ = PdV + dU = TdS , dS — изменение энтропии, T — абсолютная температура. Для идеального газа при изобарном процессе объём пропорционален температуре (закон Гей-Люссака) в реальных газах часть теплоты расходуется на изменение средней энергии взаимодействия частиц. Работа, совершаемая при изобарных процессах равна произведению внешнего давления на изменение объёма, а для обратимых изобарных процессов внешнее давление равно внутреннему. Изменение энтропии при обратимом изобарном процессе равно

где C_p — теплоёмкость при постоянном давлении.

Wikimedia Foundation . 2010 .

Смотреть что такое «Изобарический процесс» в других словарях:

изобарический процесс — izobarinis vyksmas statusas T sritis fizika atitikmenys: angl. isobaric process vok. isobare Zustandsänderung, f; isobarer Prozeß, m rus. изобарический процесс, m pranc. processus isobare, m … Fizikos terminų žodynas

изобарический процесс — izobarinis procesas statusas T sritis Energetika apibrėžtis Termodinaminis procesas, vykstantis esant pastoviajam sistemos slėgiui. atitikmenys: angl. isobaric process vok. isobarer Prozeß, m rus. изобарический процесс, m pranc. processus isobare … Aiškinamasis šiluminės ir branduolinės technikos terminų žodynas

изобарический процесс — [isobaric process] процесс в физической системе при постоянном внешнем давлении. Объем идеального газа при изобарическом процессе пропорционален температуре (закон Гей Люссака). Теплоемкость системы в изобарическом процесс больше, чем в изохорном … Энциклопедический словарь по металлургии

ИЗОБАРИЧЕСКИЙ ПРОЦЕСС — изобарный процесс, термодинамический процесс, протекающий при пост. давлении. Примеры процессов, близких к И. п.: образование пара в паровом котле, сгорание топлива в компрессорном и прямоточном воздушно реактивных двигателях, мн. процессы в хим … Большой энциклопедический политехнический словарь

Процесс — (Process) Определение процесса, виды и типы процессов Информация об определении процесса, виды и типы процессов Содержание Содержание Определение Исторический Бизнес процесс Тепловой процесс Адиабатический процесс Изохорный процесс Изобарный… … Энциклопедия инвестора

процесс жидкофазного восстановления железа (ПЖВ) — [liquid phase iron reduction process, Ro melt process] «Российская плавка», способ выплавки передельного чугуна в бесшахтной печи на некоксовом угле из неокускованной шихты. Предложен профессорами В. А. Роменцом, А. В. Ванкжовым и Е. Ф. Вегманом… … Энциклопедический словарь по металлургии

Процесс — [process]: Смотри также: электросталеплавильный процесс цементационный процесс хлоридовозгоночный процесс томасовский процесс … Энциклопедический словарь по металлургии

ИЗОБАРНЫЙ ПРОЦЕСС — (изобарический процесс), термодинамич. процесс, протекающий при пост. давлении в системе … Естествознание. Энциклопедический словарь

термодинамический процесс — [thermodynamic process] процесс в макроскопической системе, связанный с переходом ее из одного равновесного состояния в другое в результате внешних воздействий. Различают следующие основные виды термодинамического процесса: адиабатный,… … Энциклопедический словарь по металлургии

изобарный процесс — (изобарический процесс), термодинамический процесс, протекающий при постоянном давлении в системе. * * * ИЗОБАРНЫЙ ПРОЦЕСС ИЗОБАРНЫЙ ПРОЦЕСС (изобарический процесс) (от изо. (см. ИЗО. (часть сложных слов)) и baros тяжесть), термодинамический… … Энциклопедический словарь