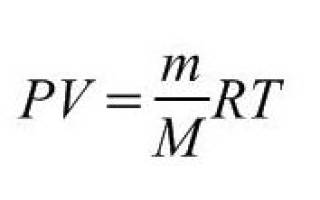Как найти плотность вещества через давление

Связь между давлением, температурой, объемом и количеством молей газа («массой» газа). Универсальная (молярная) газовая постоянная R. Уравнение Клайперона-Менделеева = уравнение состояния идеального газа.

Связь между давлением, температурой, объемом и количеством молей газа («массой» газа). Универсальная (молярная) газовая постоянная R. Уравнение Клайперона-Менделеева = уравнение состояния идеального газа.

Ограничения практической применимости:

температуры ниже -100°C и выше температуры диссоциации / разложения
давления выше 90 бар
вакуум глубже чем 99%

Внутри диапазона точность уравнения превосходит точность обычных современных инженерных средств измерения. Для инженера важно понимать, что для всех газов возможна существенная диссоциация или разложение при повышении температуры.

в СИ R= 8,3144 Дж/(моль*К) — это основная (но не единственная) инженерная система измерений в РФ и большинстве стран Европы
в СГС R= 8,3144*10 7 эрг/(моль*К) — это основная (но не единственная) научная система измерений в мире
m-масса газа в (кг)
M-молярная масса газа кг/моль (таким образом (m/M) — число молей газа)
P-давление газа в (Па)
Т-температура газа в ( °K)
V-объем газа в м 3

Давайте решим парочку задач относительно газовых объемных и массовых расходов в предположении, что состав газа не изменяется (газ не диссоциирует) — что верно для большинства газов в указанных выше пределах применимости.

1) Доставка объемов газа одинаковой массы при одинаковом давлении но различных температурах.

Данная задача актуальна в основном, но не только, для применений и устройств, в которых напрямую измеряется объем газа.

Пусть счетчик (расходомер) в точке доставки дает объемные накопленные расходы V₁ и V₂, при температурах, соответственно, T₁ и T₂ и, пусть T₁ V₂ для одинаковых количеств газа при данных условиях. Попробуем сформулировать несколько важных на практике выводов для данного случая:

показатели объемного счетчика газа тем «весомее», чем выше давление
выгодно поставлять газ низкого давления
выгодно покупать газ высокого давления

Как с этим бороться? Необходима хотя бы простая компенсация по давлению, т.е в считающее устройство должна подаваться информация с дополнительного датчика давления.

Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.

Калькулятор ниже предназначен для решения задач на использование уравнения Клапейрона-Менделеева, или уравнение состояния идеального газа. Некоторая теория изложена под калькулятором, ну а чтобы было понятно, о чем идет речь — пара примеров задач:

Примеры задач на уравнение Менделеева-Клапейрона

В колбе объемом 2,6 литра находится кислород при давлении 2,3 атмосфер и температуре 26 градусов Цельсия .
Вопрос: сколько молей кислорода содержится в колбе?

Некоторое количество гелия при 78 градусах Цельсия и давлении 45,6 атмосфер занимает объем 16,5 литров.
Вопрос: Каков объем этого газа при нормальных условиях? (Напомню, что нормальными условиями для газов считается давление в 1 атмосферу и температура 0 градусов Цельсия)

В калькулятор вводим начальные условия, выбираем, что считать (число моль, новые объем, температуру или давление), заполняем при необходимости оставшиеся условия, и получаем результат.

Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.

Теперь немного формул.

где
P — давление газа (например, в атмосферах)
V — объем газа (в литрах);
T — температура газа (в кельвинах);
R — газовая постоянная (0,0821 л·атм/моль·K).
Если используется СИ, то газовая постоянная равна 8,314 Дж/K·моль

Так как m-масса газа в (кг) и M-молярная масса газа кг/моль, то m/M — число молей газа, и уравнение можно записать также

где n — число молей газа

И как нетрудно заметить, соотношение

есть величина постоянная для одного и того же количества моль газа.

И эту закономерность опытным путем установили еще до вывода уравнения. Это так называемые газовые законы — законы Бойля-Мариотта, Гей-Люссака, Шарля.

Так, закон Бойля-Мариотта гласит (это два человека):
Для данной массы газа m при неизменной температуре Т произведение давления на объем есть величина постоянная.

Закон Гей-Люссака (а вот это один человек):
Для данной массы m при постоянном давлении P объем газа линейно зависит от температуры

Закон Шарля:
Для данной массы m при постоянном объеме V давление газа линейно зависит от температуры

Посмотрев на уравнение, нетрудно убедиться в справедливости этих законов.

Уравнение Менделеева-Клапейрона, также как и опытные законы Бойля-Мариотта, Гей-Люссака и Шарля справедливы для широкого интервала давлений, объемов и температур. То есть во многих случаях эти законы удобны для практического применения. Однако не стоит забывать, что когда давления превышают атмосферное в 300-400 раз, или температуры очень высоки, наблюдаются отклонения от этих законов.
Собственно, идеальный газ потому и называют идеальным, что по определению это и есть газ, для которого не существует отклонений от этих законов.

Глава 2. Расчет физико-химических свойств и состава углеводородных газов

Расчет физико-химических свойств и состава углеводородных газов

2.1 Особенности расчета физико-химических свойств газовых смесей. Плотность газов

Общие свойства газовых смесей. По сравнению с молекулами жидкости молекулы газов удалены друг от друга на неизмеримо большие расстояния, чем их собственные размеры. С этим связаны некоторые особые свойства газов, например способность к сжатию со значительным изменением объема, заметное повышение давления с ростом температуры и т.д. Поведение газообразных веществ достаточно полно объясняет кинетическая теория газов, основу которой составляют законы газового состояния Бойля-Мариотта, Гей-Люссака и Шарля [10]. Эти законы могут быть выражены объединенным уравнением (законом) Клайперона-Менделеева

Здесь R – универсальная газовая постоянная, значение которой зависит от выбора системы единиц. Так, в СИ, где давление выражено в паскалях, объем – в кубических метрах и температура – в кельвинах, для одного моля газа R=8,314 Дж/(моль×К).

Зависимость между парциальными давлениями p_i компонентов газовой смеси и общим давлением p в системе устанавливается законом Дальтона

где .

В соответствии с законом Рауля в условиях равновесия можно записать

или (см. уравнением 1.10) .

Приведенные выше законы полностью справедливы для идеальных газов. Углеводородные газы и нефтяные пары можно приближенно считать идеальными газами, особенно при невысоких давлениях. При расчетах допустимо использовать все названные законы. Об особых случаях расчета будет сказано ниже.

Напомним, что в приложении к газам существуют нормальные и стандартные условия, которые при одном и том же давлении (101,3 кПа) отличаются только температурой (273 К и 293 К, соответственно для нормальных и стандартных условий). Параметры, характеризующие состояние газа в нормальных условиях, имеют индекс 0 (V, p, T), в стандартных – 20 (V₂₀, p₂₀, T₂₀). Приведение объема газа к нормальным или стандартным условиям легко осуществляется по формулам:

Читать еще: Атмосферное давление в пицунде

Пример 2.1 В баллоне вместимостью 0,2 м 3 при давлении 3×10 5 Па и температуре 20°С находится газовая смесь, средняя молярная масса которой М=48 г/моль. Определить массу газовой смеси.

Решение. Зная, что число молей равно отношению массы вещества к его молярной массе, запишем уравнение Клапейрона-Менделеева в виде pV=(m/M)RT. Выразим массу газа m: m=pVM/RT. Подставив известные значения параметров, определим массу газа:

Пример 2.2 Газ при давлении 230 кПа и температуре 46°С занимает объем 1,5 м 3 . Привести объем газа к нормальным условиям.

Решение. Нормальный объем газа определим, имея в виду, что Т=273 К и р=101,3 кПа,

Плотность. Как и для жидкости, плотность газа может быть выражена абсолютным или относительным значением. Абсолютная плотность газа равна его массе в единице объема, в СИ она выражается в килограммах на кубический метр (кг/м 3 ). Величину, обратную плотности, называют удельным объемом и измеряют в кубических метрах на килограмм (м 3 /кг).

При определении относительной плотности газов и паров нефтепродуктов в качестве стандартного вещества берется воздух при нормальных условиях (Т=273 К, r=101,3 кПа). Отношение массы газа m к массе воздуха m_в, взятых в одинаковых объемах и при тех же температуре и давлении, дает относительную плотность газа:

Масса любого идеального газа при нормальных условиях равна его молярной массе, поделенной на объем, занимаемый одним молем, т.е. , где — плотность газа при нормальных условиях.

Тогда для относительной плотности газа по воздуху можно записать – молярная масса воздуха, г/моль.

Если записать уравнение Клапейрона-Менделеева в виде m/V=pM/RТ, нетрудно увидеть, что левая часть представляет собой плотность газа r, т.е.

Формула (2.2) дает возможность подсчитать истинную плотность газа при любых температуре и давлении.

Существует другая модификация уравнения Клапейрона-Менделеева, также позволяющая определить плотность газа при любых условиях:

(2.3)

Результаты, получаемые по формулам (2.2) и (2.3), одинаковы. Плотность некоторых индивидуальных газов в зависимости от изменения температуры можно, кроме того, найти по графикам и таблицам [11].

Пример 2.3. Относительная плотность газа равна 1,10. Определить его абсолютную плотность при 150°С и 750 кПа.

Решение. Найдем молярную массу газа:

Абсолютную плотность газа определим по формуле (2.3):

Тот же ответ получим, воспользовавшись формулой (2.2), однако в этом случае нужно выразить М в килограммах на моль (умножить на 10 -3 ), чтобы привести в соответствие с единицами измерения универсальной газовой постоянной.

Плотность газовой смеси может быть подсчитана по формулам для жидкой смеси (см.§1.2). Учитывая, что для газов объемные доли равны молярным, в приложении к газовой смеси можно записать

Значения плотности и некоторых других свойств индивидуальных газов приведены в прил.16.

ЗАДАЧИ

2.1. Определить вместимость баллона, в который можно закачать
6 м 3 газа, измеренного при нормальных условиях. Максимальное давление в баллоне 15 МПа.

2.2. Во сколько раз возрастет давление в герметичном газовом резервуаре, если температура окружающего воздуха повысится с 10 до 24°С?

2.3. При давлении 360 кПа и температуре 400 К газ занимает объем 1,2 м 3 . Найти число молей газа.

2.4. Газ в количестве 9 кг находится в сосуде вместимостью 3 м 3 при 298 К и 462 кПа. Найти молярную массу газа.

2.5. Определить объем газа при нормальных условиях, если при температуре 120°С и давлении 790 кПа его объем равен 16,3 м 3 .

2.6. Используя уравнение (2.1), найти плотность метана и этана при нормальных условиях.

2.7. Определить плотность пропана при 150 кПа и 80°С.

2.8. Средняя молярная масса водородсодержащего газа, применяемого в процессе каталитического риформинга, равна 3,5 г/моль. Рассчитать плотность этого газа при 450°С и 3 МПа.

2.9. Газовая смесь состоит из метана и водорода, парциальные давления которых равны Определить содержание (в молярных долях) компонентов смеси.

2.10. Рассчитать плотность газовой смеси, состоящей из 14 кг пропана, 11 кг этана и 8 кг этилена. Плотности индивидуальных газов взять в прил.16.

2.11. Смешали 3 моля пропана и 7 молей пропилена. Какова плотность полученной смеси?

2.12. Относительная плотность газовой смеси по воздуху равна 1,3. При какой температуре абсолютная плотность станет равной 7 кг/м 3 , если давление в системе составляет 640 кПа?

2.13. Природный газ Астраханского происхождения имеет следующий состав (в объемных процентах): СН₄ – 47,48; С₂Н₆ – 1,92; С₃Н₈ – 0,93; С₄Н₁₀ – 0,56; С₅Н₁₂ –3,08; N₂ –1,98; СО₂ – 21,55; Н₂S – 22,5. Определить плотность газа при нормальных условиях.

93.79.221.197 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Формула плотности газа

4 сообщения в этой теме

Создайте аккаунт или авторизуйтесь, чтобы оставить комментарий

Комментарии могут оставлять только зарегистрированные пользователи

Создать аккаунт

Зарегистрировать новый аккаунт.

Есть аккаунт? Войти.

Недавно просматривали 0 пользователей

Ни один зарегистрированный пользователь не просматривает эту страницу.

Физика (7 класс)/Давление

Содержание

Давление. Единицы давления.

По рыхлому снегу человек идёт с большим трудом, глубоко проваливаясь при каждом шаге. Но, надев лыжи, он может идти, почти не проваливаясь в него. Почему? На лыжах или без лыж человек действует на снег с одной и той же силой, равной своему весу. Однако действие этой силы в обоих случаях различно, потому что различна площадь поверхности, на которую давит человек, с лыжами и без лыж. Площадь поверхности лыж почти в 20 раз больше площади подошвы. Поэтому, стоя на лыжах, человек действует на каждый квадратный сантиметр площади поверхности снега с силой, в 20 раз меньшей, чем стоя на снегу без лыж.

Ученик, прикалывая кнопками газету к доске, действует на каждую кнопку с одинаковой силой. Однако кнопка, имеющая более острый конец, легче входит в дерево.

Значит, результат действия силы зависит не только от её модуля, направления и точки приложения, но и от площади той поверхности, к которой она приложена (перпендикулярно которой она действует).

Этот вывод подтверждают физические опыты.

По углам небольшой доски надо вбить гвозди. Сначала гвозди, вбитые в доску, установим на песке остриями вверх и положим на доску гирю. В этом случае шляпки гвоздей лишь незначительно вдавливаются в песок. Затем доску перевернем и поставим гвозди на острие. В этом случае площадь опоры меньше, и под действием той же силы гвозди значительно углубляются в песок.

От того, какая сила действует на каждую единицу площади поверхности, зависит результат действия этой силы.

В рассмотренных примерах силы действовали перпендикулярно поверхности тела. Вес человека был перпендикулярен поверхности снега; сила, действовавшая на кнопку, перпендикулярна поверхности доски.

Величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности, называется давлением.

Чтобы определить давление, надо силу, действующую перпендикулярно поверхности, разделить на площадь поверхности:

давление = сила / площадь.

Обозначим величины, входящие в это выражение: давление — p, сила, действующая на поверхность, — F и площадь поверхности — S.

Тогда получим формулу:

Понятно, что бóльшая по значению сила, действующую на ту же площадь, будет производить большее давление.

За единицу давления принимается такое давление, которое производит сила в 1 Н, действующая на поверхность площадью 1 м 2 перпендикулярно этой поверхности.

Единица давления — ньютон на квадратный метр ( 1 Н / м 2 ). В честь французского ученого Блеза Паскаля она называется паскалем (Па). Таким образом,

Используется также другие единицы давления: гектопаскаль (гПа) и килопаскаль (кПа).

Пример. Рассчитать давление, производимое на пол мальчиком, масса которого 45 кг, а площадь подошв его ботинок, соприкасающихся с полом, равна 300 см 2 .

Запишем условие задачи и решим её.

Дано: m = 45 кг, S = 300 см 2 ; p = ?

В единицах СИ: S = 0,03 м 2

P = 9,8 Н · 45 кг ≈ 450 Н,

p = 450/0,03 Н / м 2 = 15000 Па = 15 кПа

‘Ответ’: p = 15000 Па = 15 кПа

Способы уменьшения и увеличения давления.

Тяжелый гусеничный трактор производит на почву давление равное 40 — 50 кПа, т. е. всего в 2 — 3 раза больше, чем давление мальчика массой 45 кг. Это объясняется тем, что вес трактора распределяется на бóльшую площадь за счёт гусеничной передачи. А мы установили, что чем больше площадь опоры, тем меньше давление, производимое одной и той же силой на эту опору.

В зависимости от того, нужно ли получить малое или большое давление, площадь опоры увеличивается или уменьшается. Например, для того, чтобы грунт мог выдержать давление возводимого здания, увеличивают площадь нижней части фундамента.

Шины грузовых автомобилей и шасси самолетов делают значительно шире, чем легковых. Особенно широкими делают шины у автомобилей, предназначенных для передвижения в пустынях.

Тяжелые машины, как трактор, танк или болотоход, имея большую опорную площадь гусениц, проходят по болотистой местности, по которой не пройдет человек.

С другой стороны, при малой площади поверхности можно небольшой силой произвести большое давление. Например, вдавливая кнопку в доску, мы действуем на нее с силой около 50 Н. Так как площадь острия кнопки примерно 1 мм 2 , то давление, производимое ею, равно:

p = 50 Н/ 0, 000 001 м 2 = 50 000 000 Па = 50 000 кПа.

Для сравнения, это давление в 1000 раз больше давления, производимого гусеничным трактором на почву. Можно найти еще много таких примеров.

Лезвие режущих и острие колющих инструментов (ножей, ножниц, резцов, пил, игл и др.) специально остро оттачивается. Заточенный край острого лезвия имеет маленькую площадь, поэтому при помощи даже малой силы создается большое давление, и таким инструментом легко работать.

Режущие и колющие приспособления встречаются и в живой природе: это зубы, когти, клювы, шипы и др. — все они из твердого материала, гладкие и очень острые.

Мы уже знаем, что газы, в отличие от твердых тел и жидкостей, заполняют весь сосуд, в котором находятся. Например, стальной баллон для хранения газов, камера автомобильной шины или волейбольный мяч. При этом газ оказывает давление на стенки, дно и крышку баллона, камеры или любого другого тела, в котором он находится. Давление газа обусловлено иными причинами, чем давление твердого тела на опору.

Известно, что молекулы газа беспорядочно движутся. При своем движении они сталкиваются друг с другом, а также со стенками сосуда, в котором находится газ. Молекул в газе много, поэтому и число их ударов очень велико. Например, число ударов молекул воздуха, находящегося в комнате, о поверхность площадью 1 см 2 за 1 с выражается двадцатитрехзначным числом. Хотя сила удара отдельной молекулы мала, но действие всех молекул на стенки сосуда значительно, — оно и создает давление газа.

Итак, давление газа на стенки сосуда (и на помещенное в газ тело) вызывается ударами молекул газа.

Рассмотрим следующий опыт. Под колокол воздушного насоса поместим резиновый шарик. Он содержит небольшое количество воздуха и имеет неправильную форму. Затем насосом откачиваем воздух из-под колокола. Оболочка шарика, вокруг которой воздух становится все более разреженным, постепенно раздувается и принимает форму правильного шара.

Как объяснить этот опыт?

Читать еще: Ишемия последствия для организма

В нашем опыте движущиеся молекулы газа непрерывно ударяют о стенки шарика внутри и снаружи. При откачивании воздуха число молекул в колоколе вокруг оболочки шарика уменьшается. Но внутри шарика их число не изменяется. Поэтому число ударов молекул о внешние стенки оболочки становится меньше, чем число ударов о внутренние стенки. Шарик раздувается до тех пор, пока сила упругости его резиновой оболочки не станет равной силе давления газа. Оболочка шарика принимает форму шара. Это показывает, что газ давит на ее стенки по всем направлениям одинаково. Иначе говоря, число ударов молекул, приходящихся на каждый квадратный сантиметр площади поверхности, по всем направлениям одинаково. Одинаковое давление по всем направлениям характерно для газа и является следствием беспорядочного движения огромного числа молекул.

Попытаемся уменьшить объем газа, но так, чтобы масса его осталась неизменной. Это значит, что в каждом кубическом сантиметре газа молекул станет больше, плотность газа увеличится. Тогда число ударов молекул о стенки увеличится, т. е. возрастет давление газа. Это можно подтвердить опытом.

На рисунке а изображена стеклянная трубка, один конец которой закрыт тонкой резиновой пленкой. В трубку вставлен поршень. При вдвигании поршня объем воздуха в трубке уменьшается, т. е. газ сжимается. Резиновая пленка при этом выгибается наружу, указывая на то, что давление воздуха в трубке увеличилось.

Наоборот, при увеличении объема этой же массы газа, число молекул в каждом кубическом сантиметре уменьшается. От этого уменьшится число ударов о стенки сосуда — давление газа станет меньше. Действительно, при вытягивании поршня из трубки объем воздуха увеличивается, пленка прогибается внутрь сосуда. Это указывает на уменьшение давления воздуха в трубке. Такие же явления наблюдались бы, если бы вместо воздуха в трубке находился бы любой другой газ.

Итак, при уменьшении объема газа его давление увеличивается, а при увеличении объема давление уменьшается при условии, что масса и температура газа остаются неизменными.

А как изменится давление газа, если нагреть его при постоянном объеме? Известно, что скорость движения молекул газа при нагревании увеличивается. Двигаясь быстрее, молекулы будут ударять о стенки сосуда чаще. Кроме того, каждый удар молекулы о стенку будет сильнее. Вследствие этого, стенки сосуда будут испытывать большее давление.

Следовательно, давление газа в закрытом сосуде тем больше, чем выше температура газа, при условии, что масса газа и объем не изменяются.

Из этих опытов можно сделать общий вывод, что давление газа тем больше, чем чаще и сильнее молекулы ударяют о стенки сосуда.

Для хранения и перевозки газов их сильно сжимают. При этом давление их возрастает, газы необходимо заключать в специальные, очень прочные баллоны. В таких баллонах, например, содержат сжатый воздух в подводных лодках, кислород, используемый при сварке металлов. Конечно же, мы должны навсегда запомнить, что газовые баллоны нельзя нагревать, тем более, когда они заполнены газом. Потому что, как мы уже понимаем, может произойти взрыв с очень неприятными последствиями.

Закон Паскаля.

В отличие от твердых тел отдельные слои и мелкие частицы жидкости и газа могут свободно перемещаться относительно друг друга по всем направлениям. Достаточно, например, слегка подуть на поверхность воды в стакане, чтобы вызвать движение воды. На реке или озере при малейшем ветерке появляется рябь.

Подвижностью частиц газа и жидкости объясняется, что давление, производимое на них, передается не только в направлении действия силы, а в каждую точку. Рассмотрим это явление подробнее.

На рисунке, а изображен сосуд, в котором содержится газ (или жидкость). Частицы равномерно распределены по всему сосуду. Сосуд закрыт поршнем, который может перемещаться вверх и вниз.

Прилагая некоторую силу, заставим поршень немного переместиться внутрь и сжать газ (жидкость), находящийся непосредственно под ним. Тогда частицы (молекулы) расположатся в этом месте более плотно, чем прежде(рис, б). Благодаря подвижности частицы газа будут перемещаться по всем направлениям. Вследствие этого их расположение опять станет равномерным, но более плотным, чем раньше (рис, в). Поэтому давление газа всюду возрастет. Значит, добавочное давление передается всем частицам газа или жидкости. Так, если давление на газ (жидкость) около самого поршня увеличится на 1 Па, то во всех точках внутри газа или жидкости давление станет больше прежнего на столько же. На 1 Па увеличится давление и на стенки сосуда, и на дно, и на поршень.

Давление, производимое на жидкость или газ, передается на любую точку одинаково во всех направлениях.

Это утверждение называется законом Паскаля.

На основе закона Паскаля легко объяснить следующие опыты.

На рисунке изображен полый шар, имеющий в различных местах небольшие отверстия. К шару присоединена трубка, в которую вставлен поршень. Если набрать воды в шар и вдвинуть в трубку поршень, то вода польется из всех отверстий шара. В этом опыте поршень давит на поверхность воды в трубке. Частицы воды, находящиеся под поршнем, уплотняясь, передают его давление другим слоям, лежащим глубже. Таким образом, давление поршня передается в каждую точку жидкости, заполняющей шар. В результате часть воды выталкивается из шара в виде одинаковых струек, вытекающих из всех отверстий.

Если шар заполнить дымом, то при вдвигании поршня в трубку из всех отверстий шара начнут выходить одинаковые струйки дыма. Это подтверждает, что и газы передают производимое на них давление во все стороны одинаково.

Давление в жидкости и газе.

На жидкости, как и на все тела на Земле, действует сила тяжести. Поэтому, каждый слой жидкости, налитой в сосуд, своим весом создает давление, которое по закону Паскаля передается по всем направлениям. Следовательно, внутри жидкости существует давление. В этом можно убедиться на опыте.

В стеклянную трубку, нижнее отверстие которой закрыто тонкой резиновой пленкой, нальем воду. Под действием веса жидкости дно трубки прогнется.

Опыт показывает, что, чем выше столб воды над резиновой пленкой, тем больше она прогибается. Но всякий раз после того, как резиновое дно прогнулось, вода в трубке приходит в равновесие (останавливается), так как, кроме силы тяжести, на воду действует сила упругости растянутой резиновой пленки.