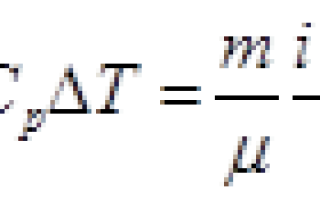В сосуде объемом при давлении
В сосуде объемом 2 л находится гелий при давлении 100 кПа и температуре 200 К
Условие задачи:
В сосуде объемом 2 л находится гелий при давлении 100 кПа и температуре 200 К, а в сосуде объемом 5 л — неон при давлении 200 кПа и температуре 500 К. Определить температуру газа в сосудах после соединения их трубкой.
Задача №5.4.35 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
(V_1=2) л, (p_1=100) кПа, (T_1=200) К, (V_2=5) л, (p_2=200) кПа, (T_2=500) К, (T-?)
Решение задачи:
После смешения газов их давление и температура станет одинаковой. Запишем уравнение Клапейрона-Менделеева для гелия и неона до смешения и для смеси газов после смешения:
Для решения этой задачи нужно понимать тот факт, что суммарная внутренняя энергия двух указанных газов после соединения сосудов трубкой не изменится. Почему? Дело в том, что внутреннюю энергию газа можно изменить передачей количества теплоты или совершением работы (обратитесь к первому закону термодинамики, чтобы убедиться в этом), но ни первого, ни второго при соединении сосудов с газами не произойдёт. Поэтому:
Распишем внутренние энергии по известным формулам:
Учитывая уравнения (1)-(3), последнее равенство примет вид:
Тогда уравнение (3) можно записать в следующем виде:
Количество вещества гелия (nu_1) и неона (nu_2) выразим из уравнений (1) и (2):
Полученные выражения подставим в формулу (4):
В правой части этого равенства в скобках приведём под общий знаменатель:
И наконец последнее действие — выразим искомую температуру (T):
Переведём объемы гелия (V_1) и неона (V_2) в систему СИ:
Посчитаем численный ответ:
[T = frac<Ответ: 127 °C.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
В сосуде объемом при давлении
Решение:
К оличество теплоты для изобарного процесса
Из уравнения Менделеева-Клапейрона
и подставим в выражение для Q 1
К оличество теплоты для изохорного процесса
Из уравнения Менделеева-Клапейрона
и подставим в выражение для Q 2
Ответ:
В сосуде объемом при давлении
В сосуд объёмом V = 10 дм 3 , наполненный сухим воздухом при давлении ро = 10 5 Па и температуре То = 273 К, вводят m = 3 г воды. Сосуд нагревают до температуры Т = 373 К. Каково давление влажного воздуха в сосуде при этой температуре? Молярная масса воздуха М = 0,029 кг/моль, давление насыщенного пара пара при температуре Т = 373 К р = 101330 Па.
Выпишем соответствующие формулы:
— Уравнение Менделеева-Клапейрона.
По закону Дальтона давление влажного воздуха будет складываться из нового давления сухого воздуха р1 и давления водяных паров р2.
Найдём давление сухого воздуха:
Проверим, испарится ли вся вода. Давление насыщенного пара при Т = 373 К рн = 10133 Па. Найдём для нашего условия массу испарившейся при этом воды m1:
Видим, что m1 > m, следовательно, испарится вся вода и в сосуде будет находиться насыщенный пар с давлением рн = 101330 Па.
р = 32065 + 101330 = 133395 Па.
73% выпускников не работают по специальности, потому что.
— Выбрали профессию, опираясь только на опыт друзей и родителей
— Не учли свои личностные особенности, способности и интересы
— Выбрали вуз, опираясь только на баллы ЕГЭ
Давление газа — формула. Формула давления газа в сосуде
Давление является одним из трех основных термодинамических макроскопических параметров любой газовой системы. В данной статье рассмотрим формулы давления газа в приближении идеального газа и в рамках молекулярно-кинетической теории.
Идеальные газы
Каждый школьник знает, что газ является одним из четырех (включая плазму) агрегатных состояний материи, в котором частицы не имеют определенных положений и движутся хаотичным образом во всех направлениях с одинаковой вероятностью. Исходя из такого строения, газы не сохраняют ни объем, ни форму при малейшем внешнем силовом воздействии на них.
В любом газе средняя кинетическая энергия его частиц (атомов, молекул) больше, чем энергия межмолекулярного взаимодействия между ними. Кроме того, расстояния между частицами намного превышают их собственные размеры. Если молекулярными взаимодействиями и размерами частиц можно пренебречь, тогда такой газ называется идеальным.
В идеальном газе существует лишь единственный вид взаимодействия — упругие столкновения. Поскольку размер частиц пренебрежимо мал в сравнении с расстояниями между ними, то вероятность столкновений частица-частица будет низкой. Поэтому в идеальной газовой системе существуют только столкновения частиц со стенками сосуда.
Все реальные газы с хорошей точностью можно считать идеальными, если температура в них выше комнатной, и давление не сильно превышает атмосферное.
Причина возникновения давления в газах
Прежде чем записать формулы расчета давления газа, необходимо разобраться, почему оно возникает в изучаемой системе.
Согласно физическому определению, давление – это величина, равная отношению силы, которая перпендикулярно воздействует на некоторую площадку, к площади этой площадки, то есть:
Выше мы отмечали, что существует только один единственный тип взаимодействия в идеальной газовой системе – это абсолютно упругие столкновения. В результате них частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. Для этого случая применим второй закон Ньютона:
Именно сила F приводит к появлению давления на стенки сосуда. Сама величина F от столкновения одной частицы является незначительной, однако количество частиц огромно (≈ 10 23 ), поэтому они в совокупности создают существенный эффект, который проявляется в виде наличия давления в сосуде.
Формула давления газа идеального из молекулярно-кинетической теории
При объяснении концепции идеального газа выше были озвучены основные положения молекулярно-кинетической теории (МКТ). Эта теория основывается на статистической механике. Развита она была во второй половине XIX века такими учеными, как Джеймс Максвелл и Людвиг Больцман, хотя ее основы заложил еще Бернулли в первой половине XVIII века.
Согласно статистике Максвелла-Больцмана, все частицы системы движутся с различными скоростями. При этом существует малая доля частиц, скорость которых практически равна нулю, и такая же доля частиц, имеющих огромные скорости. Если вычислить среднюю квадратичную скорость, то она примет некоторую величину, которая в течение времени остается постоянной. Средняя квадратичная скорость частиц однозначно определяет температуру газа.
Применяя приближения МКТ (невзаимодействующие безразмерные и хаотично перемещающиеся частицы), можно получить следующую формулу давления газа в сосуде:
Здесь N – количество частиц в системе, V – объем, v – средняя квадратичная скорость, m – масса одной частицы. Если все указанные величины определены, то, подставив их в единицах СИ в данное равенство, можно рассчитать давление газа в сосуде.
Формула давления из уравнения состояния
В середине 30-х годов XIX века французский инженер Эмиль Клапейрон, обобщая накопленный до него экспериментальный опыт по изучению поведения газов во время разных изопроцессов, получил уравнение, которое в настоящее время называется универсальным уравнением состояния идеального газа. Соответствующая формула имеет вид:
Здесь n – количество вещества в молях, T – температура по абсолютной шкале (в кельвинах). Величина R называется универсальной газовой постоянной, которая была введена в это уравнение русским химиком Д. И. Менделеевым, поэтому записанное выражение также называют законом Клапейрона-Менделеева.
Из уравнения выше легко получить формулу давления газа:
Равенство говорит о том, что давление линейно возрастает с температурой при постоянном объеме и увеличивается по гиперболе с уменьшением объема при постоянной температуре. Эти зависимости отражены в законах Гей-Люссака и Бойля-Мариотта.
Если сравнить это выражение с записанной выше формулой, которая следует из положений МКТ, то можно установить связь между кинетической энергией одной частицы или всей системы и абсолютной температурой.
Давление в газовой смеси
Отвечая на вопрос о том, как найти давление газа и формулы, мы ничего не говорили о том, является ли газ чистым, или речь идет о газовой смеси. В случае формулы для P, которая следует из уравнения Клапейрона, нет никакой связи с химическим составом газа, в случае же выражения для P из МКТ эта связь присутствует (параметр m). Поэтому при использовании последней формулы для смеси газов становится непонятным, какую массу частиц выбирать.
Когда необходимо рассчитать давление смеси идеальных газов, следует поступать одним из двух способов:
- Рассчитывать среднюю массу частиц m или, что предпочтительнее, среднее значение молярной массы M, исходя из атомных процентов каждого газа в смеси;
- Воспользоваться законом Дальтона. Он гласит, что давление в системе равно сумме парциальных давлений всех ее компонентов.
Пример задачи
Известно, что средняя скорость молекул кислорода составляет 500 м/с. Необходимо определить давление в сосуде объемом 10 литров, в котором находится 2 моль молекул.
Ответ на задачу можно получить, если воспользоваться формулой для P из МКТ:
Здесь содержатся два неудобных для выполнения расчетов параметра – это m и N. Преобразуем формулу следующим образом:
Объем сосуда в кубических метрах равен 0,01 м 3 . Молярная масса молекулы кислорода M равна 0,032 кг/моль. Подставляя в формулу эти значения, а также величины скорости v и количества вещества n из условия задачи, приходим к ответу: P = 533333 Па, что соответствует давлению в 5,3 атмосферы.
Примеры решения задач
Скачивание файла
Введите число с картинки:
1 ТЕХНИЧЕСКАЯ ТЕРМОДИНАМИКА
Параметры состояния тела
Примеры решения задач
1. Давление воздуха по ртутному барометру равно 770 мм при 0° С. Выразить это давление в барах и Па.
1мм рт. ст. = 133,3 Па, 770 мм рт. ст. =102700 Па = 1,027 бар.
2. Определить абсолютное давление пара в котле, если манометр показывает Р = 1,3 бар, а атмосферное давление по ртутному барометру составляет 680 мм при t = 25° С.
Показание барометра получено при температуре t = 25° С. Это показание необходимо привести к 0 ºС по уравнению (5):
Р о = Р t (1 — 0,000172 t) = 680 · 0,9957 = 677,1 мм рт. ст.
Абсолютное давление пара в котле по формуле (3) равно
Р абс = 130000 + 677,1 * 133,3 = 0,22 МПа.
3. Давление в паровом котле Р = 0,4 бар при барометрическом давлении 725 мм рт. ст . Чему будет равно избыточное давление в котле, если показание барометра повысится до 785 мм рт. ст . , а состояние пара в котле останется прежним? Барометрическое давление приведено к 0 °С.
Абсолютное давление в котле
Р абс = 400000 + 725 * 133,3 = 136642 Па
Избыточное давление при показании барометра 785 мм рт. ст.
Р изб = 136642 – 785 * 133,3 = 32000 Па.
4. Ртутный вакуумметр, присоединенный к сосуду, показывает разрежение 420 мм при температуре ртути в вакуумметре t = 20 °С. Давление атмосферы по ртутному барометру 768 мм при температуре t = 18 °С. Определить абсолютное давление в сосуде.
Приводим показания вакуумметра и барометра к температуре ртути 0 °С (уравнение 5):
Р вак = 420 (1—0,000172 * 20) = 418,5 мм рт. ст.
Р атм = 768 (1—0,000172 * 18) = 765,6 мм рт. ст.
Абсолютное давление в сосуде по формуле (4)
Рабс = 765,6 – 418,5 = 347,1 мм рт. ст. = 46,3 кПа.
5. Водяной пар перегрет на 45 °С. Чему соответствует этот перегрев по термометру Фаренгейта?
При переводе разности температур, выраженной градусами шкалы Цельсия, в градусы Фаренгейта и наоборот надо исходить только из цены деления того и другого термометров. Поэтому формула (8) принимает следующий вид:
Следовательно, для нашего случая
Основные газовые законы
Примеры решения задач
6. Какой объем занимает 1 кг азота при температуре 70 °С и давлении 0,2 МПа .
Из характеристического уравнения для 1 кг газа (16) имеем
7. Во сколько раз объем определенной массы газа при -20 °С меньше, чем при +20°C, если давление в обоих случаях одинаковое?
При постоянном давлении объем газа изменяется по уравнению (10):
8. Определить массу 5 м 3 водорода, 5 м 3 кислорода и 5 м 3 углекислоты при давлении 6 бар и температуре 100 °С.
Характеристическое уравнение для произвольного количества газа
Значение газовой постоянной берем из табл. (приложение А). Получаем
Rн 2 . = 4124 дж/(кг·град); Rо 2 = 259,8 дж/(кг·град);
Rco 2 = 188,9 дж/(кг·град).
9. Баллон с кислородом емкостью 20 л находится под давлением 10 МПа при 15 °С. После расходования части кислорода давление понизилось до 7,6 МПа, а температура упала до 10 °С.
Определить массу израсходованного кислорода.
Из характеристического уравнения (15) имеем
Следовательно, начальная и конечная масса кислорода соответственно равны
Таким образом расход кислорода:
10. Сосуд емкостью 10 м 3 заполнен 25 кг углекислого газа. Определить абсолютное давление в сосуде, если температура в нем 27 °С.
Из характеристического уравнения (15) имеем
11. Определить подъемную силу воздушного шара, наполненного водородом, если объем его равен 1 м 3 при давлении 750 мм рт. ст . и температуре 15 °С.
На поверхности земли подъемная сила воздушного шара, наполненного водородом, равна разности сил тяжести (весов) воздуха и водорода в объеме шара:
где g = 9,81 м/сек 2 — ускорение силы тяжести на уровне земли.
Значения плотностей воздуха и водорода могут быть определены из уравнения состояния (15) :
Значения газовых постоянных могут быть легко вычислены или взяты из табл. (приложение А): R возд = 287 Дж/(кг·град); Rн 2 = 4124 Дж/(кг·град). Так как давление водорода и воздуха равно 750 мм рт. ст . , то
Следовательно, подъемная сила шара
12. Какова будет плотность окиси углерода при 20 °С и 710 мм рт. ст . , если при 0 °С и 760 мм рт. ст. она равна 1,251 кг/м 3 ?
Согласно уравнению (22)
Примеры решения задач 1 з-н т/д
24.В котельной электрической станции за 20 ч работы сожжены 62 т каменного угля, имеющего теплоту сгорания 28900 кДж/кг. Определить среднюю мощность станции, если в электрическую энергию превращено 18% тепла, полученного при сгорании угля.
Количество тепла, превращенного в электрическую энергию за 20 ч работы,
Q=62∙1000∙28900∙0,18 = 3,2∙10 9 кДж.
Эквивалентная ему электрическая энергия или работа
Следовательно, средняя электрическая мощность станции
N=89590 / 20 = 4479 кВт.
25. Паросиловая установка мощностью 4200 кВт имеет КПД равный 0,2. Определить часовой расход топлива, если его теплота сгорания равна 25000 кДж/кг.
По формуле (67) находим выражение для расхода топлива
Часовой расход топлива составит
0,72 ∙ 4200 = 3024 кг/ч.
26. Найти изменение внутренней энергии 1 кг воздуха при изменении его температуры от 300°С до 50°С. Зависимость теплоемкости от температуры принять линейной.
Изменение внутренней энергии можно определить на основании формулы (53). Рассчитаем среднюю теплоемкость воздуха в данном интервале температур (табл. В.1 приложения):
Примеры решения задач 2з-н тд
46. 1 кг кислорода при температуре 127°С расширяется до пятикратного объема; температура его при этом падает до 27ºС. Определить изменение энтропии. Теплоемкость считать постоянной.
По уравнению (100)
47. 1 кг воздуха сжимается по адиабате так, что объем его уменьшается в 6 раз, а затем при V = const давление повышается в 1,5 раза. Определить общее изменение энтропии воздуха. Теплоемкость считать постоянной.
Изменение энтропии воздуха в адиабатном процессе будет равно нулю. Изменение энтропии в изохорном процессе определится по формуле (103):
48. 10 м 3 воздуха, находящегося в начальном состоянии при нормальных условиях, сжимают до конечной температуры 400°С. Сжатие производится: 1) изохорно, 2) изобарно, 3) адиабатно и 4) политропно с показателем политропы n = 2,2. Считая значение энтропии при нормальных условиях равным нулю и принимая теплоемкость воздуха постоянной, определить энтропию воздуха в конце каждого процесса.
Находим массу 10 м 3 воздуха при нормальных условиях:
Определяем изменение энтропии в каждом из перечисленных процессов:
1) изохорное сжатие
2) изобарное сжатие
3) адиабатное сжатие
4) политропное сжатие
49. В процессе политропного расширения воздуха температура его уменьшилась от 25°С до — 37°С. Начальное давление воздуха 4 бар, количество его 2 кг. Определить изменение энтропии в этом процессе, если известно, что количество подведенного к воздуху тепла составляет 89,2 кДж .
Количество тепла, сообщаемого газу в политропном процессе на основании уравнения (85) составляет
Подставляя значения известных величин, получаем
Отсюда показатель политропы n = 1,2.
Из соотношения параметров политропного процесса определяем конечное давление:
Изменение энтропии по уравнению (101)
50. В сосуде объемом 300 л заключен воздух при давлении 50 бар и температуре 20°С. Параметры среды: Р 0 = 1 бар, t 0 = 20°С. Определить максимальную полезную работу, которую может произвести сжатый воздух, находящийся в сосуде.
Так как температура воздуха в начальном состоянии равна температуре среды, то максимальная работа, которую может выполнить воздух, может быть получена лишь при условии изотермического расширения воздуха от начального давления Р 1 = 50 бар до давления среды Р 2 = 1 бар. Максимальная полезная работа определяется на основании формулы (109):
L max (полезн) = T 0 ∙ (s 2 — s 1 ) – Р 0 ∙ (V 2 – V 1 )
L max (полезн) = m∙Т 0 ∙ (s 2 — s 1 ) — P 0 ∙ (V 2 – V 1 ).
Определяем массу воздуха, находящегося в сосуде, и объем воздуха после изотермического расширения:
Так как изменение энтропии в изотермическом процессе определяется по формуле (106)
51. Определить максимальную полезную работу, которая может быть произведена 1 кг кислорода, если его начальное состояние характеризуется параметрами t 1 = 400°С и Р 1 = 1 бар, а состояние среды — параметрами t 0 = 20ºС,Р 0 = 1 бар.
Максимальная работа, которую произведет при данных условиях кислород, может быть получена лишь при условии перехода его от начального состояния к состоянию среды обратимым путем. Так как температура кислорода в начальном состоянии выше температуры среды, то прежде всего необходимо обратимым процессом снизить температуру кислорода до температуры среды. Таким процессом может явиться только адиабатное расширение кислорода. При этом конечный объем и конечное давление определяются из следующих соотношений:
После адиабатного расширения необходимо обратимым путем при t = const сжать кислород от давления 0,0542 бар до давления окружающей среды, т. е. осуществить изотермическое сжатие кислорода до 1 бар. При этом конечный объем кислорода
Максимальная полезная работа определяется по формуле (110):
Задача может быть решена также и графическим способом –через площади на PV-диаграмме.
Примеры решения задач
52. 1 кг воздуха совершает цикл Карно (см. рис. 2) в пределах температур t 1 = 627°С и t 2 = 27 o С, причем наивысшее давление составляет 60 бар , а наинизшее — 1 бар.
Определить параметры состояния воздуха в характерных точках цикла, работу, термический КПД цикла и количество подведенного и отведенного тепла.
Точка 1: Р 1 = 60 бар; Т 1 = 900 К. Удельный объем газа определяем из характеристического уравнения (16)
Точка 2: Т 2 = 900 К. Давление находим из уравнения адиабаты (процесс 2-3)
Удельный объем находим из уравнения изотермы (процесс 1-2)
Точка 3: Р 3 = 1 бар; Т 3 = 300 К;
Точка 4: Т 4 = 300 К. Давление воздуха находим из уравнения адиабаты (процесс 4 — 1), удельный объем – из уравнения изотермы (процесс 3 — 4):
Термический КПД цикла
Подведенное количество тепла
Отведенное количество тепла
Для проверки можно воспользоваться формулой (111):
53. Для идеального цикла поршневого ДВС с подводом тепла при V = const определить параметры в характерных точках, полученную работу, термический КПД, количество подведенного и отведенного тепла, если: Р 1 =1 бар; t 1 =20 о C, = 3,6; = 3,33; k = 1,4. Рабочее тело — воздух. Теплоемкость принять постоянной.
Расчет ведем для I кг воздуха.
Точка 1: P 1 =1бар; t 1 =20 o С. Удельный объем определяем из уравнения состояния (15):
Точка 2. Удельный объем находим исходя из степени сжатия
Температура в конце адиабатного сжатия определяется из соотношения
Давление в конце адиабатного сжатия определяем по характеристическому уравнению (15)
Точка 3. Удельный объем v 3 =v 2 =0,233 м 3 /кг. Из соотношения параметров в изохорном процессе (линия 2-3) получаем
Точка 4. Удельный объем v 4 =v 1 =0,84 м 3 /кг. Температура в конце адиабатного расширения – уравнение (78)
Давление в конце адиабатного расширения определяем из соотношения параметров в изохорном процессе (линия 4-1):
Определяем количество подведенного и отведенного тепла
Термический КПД цикла определяем по формуле (111)
или по формуле (115)
54. В идеальном одноступенчатом компрессоре массовой производительностью G=180 кг/ч сжимается воздух до давления Р 2 =4,9 бар . Определить теоретически необходимую мощность электродвигателя компрессора, отведенное в рубашку цилиндра компрессора тепло и расход охлаждающей воды, если сжатие происходит политропно (п = 1,3), а охлаждающая вода нагревается на 25°С. Начальное давление воздуха Р 1 =0,98 бар и температура t 1 =0 С.
Работа, расходуемая на сжатие 1 кг газа в одноступенчатом компрессоре при политермическом режиме, определяется по формуле (125)
Мощность, расходуемая на сжатие газа в компрессоре, определяем по формуле (129)
Удельное количество отведенной теплоты определяем по формуле (85)
Температуру в конце политропного сжатия определяем из соотношения (83)
Определяем полное количество отведенной теплоты
Расход охлаждающей воды составляет
55. Определить расход воды на охлаждение воздуха в рубашке двухступенчатого компрессора производительностью 10 м 3 /мин . в промежуточном и концевом холодильниках, если в холодильниках воздух охлаждается до начальной температуры, а вода нагревается на 15 С. Воздух перед компрессором имеет давление Р 1 = 0,98 бар и температуру t 1 =10 С, сжатие воздуха в компрессоре происходит политропно (п=1,3) до конечного давления Р 2 =8,8 бар.
Количество тепла, отводимого в рубашке компрессора
от 1 кг воздуха,
от G кг воздуха
Количество тепла, отводимого в промежуточном и концевом холодильниках: от 1 кг воздуха
от G кг воздуха
Массовую производительности компрессора определяем из характеристического уравнения (15)
Промежуточное давление – уравнения (132) и (133)
Температура в конце сжатия – уравнение (83)
Количество тепла, отводимого в рубашке .компрессора,
Количество тепла, отводимого в промежуточном и концевом холодильниках,