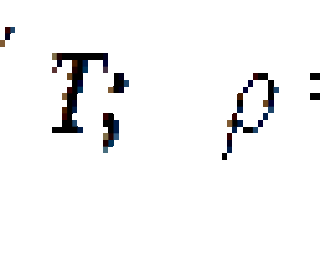Зависимость плотности газа от давления график

Плотность воздуха при различных давлениях таблица. Зависимость параметров жидкости, газа и пористой среды от давления

Выведенные дифференциальные уравнения (1.2, 1.4) содержат параметры, которые характеризуют жидкость или газ: плотность r , вязкость m , а также параметры пористой среды – коэффициенты пористости m и проницаемости k . Для дальнейших расчетов надо знать зависимость этих коэффициентов от давления.

Плотность капельной жидкости . При установившейся фильтрации капельной жидкости можно считать ее плотность, не зависящей от давления, то есть рассматривать жидкость как несжимаемую: r = const .

В неустановившихся процессах необходимо учитывать сжимаемости жидкости, которая характеризуется коэффициентом объемного сжатия жидкости b ж . Этот коэффициент обычно считают постоянным:

Проинтегрировав последнее равенство от начального значений давления р 0 и плотности r 0 до текущих значений, получим:

При этом получаем линейную зависимость плотности от давления.

Плотность газов . Сжимаемые жидкости (газы) при малых изменениях давления и температуры также можно характеризовать коэффициентами объёмного сжатия и температурного расширения. Но при больших изменениях давлений и температур эти коэффициенты меняются в больших пределах, поэтому зависимость плотности идеального газа с давлением и температурой находятся на основе уравнения состояния Клайперона – Менделеева :

где R’ = R/M m – газовая постоянная, зависящая от состава газа.

Газовая постоянная для воздуха и метана соответственно равны, R΄ воздуха = 287 Дж/кг K˚; R΄ метан = 520 Дж/кг K˚.

Последнее уравнение иногда записывают в виде:

Из последнего уравнения видно, что плотность газа зависит от давления и температуры, поэтому если известна плотность газа, то необходимо указывать давление, температуру и состав газа, что неудобно. Поэтому вводятся понятия нормальных и стандартных физических условий.

Нормальные условия соответствуют температуре t = 0°С и давлению p ат = 0,1013°МПа. Плотность воздуха при нормальных условиях равна ρ в.н.ус = 1,29 кг/м 3 .

Стандартные условия соответствуют температуре t = 20°С и давлению p ат = 0,1013°МПа. Плотность воздуха при стандартных условиях равна ρ в.ст.ус = 1,22 кг/м 3 .

Поэтому по известной плотности при данных условиях можно рассчитать плотность газа при других значениях давления и температуры:

Исключая пластовую температуру, получим уравнение состояния идеального газа, которым будем пользоваться в дальнейшем:

где z – коэффициент, характеризующий степень отклонения состояния реального газа от закона идеальных газов (коэффициент сверхсжимаемости) и зависящий для данного газа от давления и температуры z = z(p, Т) . Значения коэффициента сверхсжимаемости z определяются по графикам Д. Брауна.

Вязкость нефти . Эксперименты показывают, что коэффициенты вязкости нефти (при давлениях выше давления насыщения) и газа увеличиваются с повышением давления. При значительных изменениях давления (до 100 МПа) зависимость вязкости пластовых нефтей и природных газов от давления можно принять экспоненциальной:

При малых изменениях давления эта зависимость имеет линейный характер.

Здесь m 0 – вязкость при фиксированном давлении p 0 ; β m – коэффициент, определяемый экспериментально и зависящий от состава нефти или газа.

Пористость пласта . Чтобы выяснить, как зависит от давления коэффициент пористости, рассмотрим вопрос о напряжениях, действующих в пористой среде, заполненной жидкостью. При уменьшении давления в жидкости увеличивается силы на скелет пористой среды, поэтому пористость уменьшается.

Вследствие малой деформации твердой фазы считают обычно, что изменение пористости зависит от изменения давления линейно. Закон сжимаемости породы записывают следующим образом, вводя коэффициент объемной упругости пласта b с :

где m 0 – коэффициент пористости при давлении p 0 .

Лабораторные эксперименты для разных зернистых пород и промысловые исследования показывают, что коэффициент объемной упругости пласта составляет (0,3 – 2) 10 -10 Па -1 .

При значительных изменениях давления изменение пористости описывается уравнением:

а при больших – экспоненциальной:

В трещиноватых пластах проницаемость изменяется в зависимости от давления более интенсивно, чем в пористых, поэтому в трещиноватых пластах учет зависимости k(p) более необходим, чем в гранулярных.

Уравнения состояния жидкости или газа, насыщающих пласт, и пористой среды замыкают систему дифференциальных уравнений.

Реферат на тему:

Плотность воздуха

1 Взаимосвязи в пределах модели идеального газа
- 1.1 Температура, давление и плотность
- 1.2 Влияние влажности воздуха
- 1.3 Влияние высоты над уровнем моря в тропосфере
Примечания

Плотность воздуха — масса газа атмосферы Земли на единицу объема или удельная масса воздуха при естественных условиях. Величина плотности воздуха является функцией от высоты производимых измерений, от его температуры и влажности. Обычно стандартной величиной считается значение 1,225 кг ⁄ м 3 , которая соответствует плотности сухого воздуха при 15°С на уровне моря.

1. Взаимосвязи в пределах модели идеального газа

1.1. Температура, давление и плотность

Плотность сухого воздуха может быть вычислена с использованием уравнения Клапейрона для идеального газа при заданных температуре (англ.) русск. и давлении:

Здесь ρ — плотность воздуха, p — абсолютное давление, R — удельная газовая постоянная для сухого воздуха (287,058 Дж ⁄ (кг·К) ) , T — абсолютная температура в Кельвинах. Таким образом подстановкой получаем:

при стандартной атмосфере Международного союза теоретической и прикладной химии (температуре 0°С, давлении 100 КПа, нулевой влажности) плотность воздуха 1,2754 кг ⁄ м³ ;
при 20 °C, 101,325 КПа и сухом воздухе плотность атмосферы составляет 1,2041 кг ⁄ м³ .

В приведенной таблице даны различные параметры воздуха, вычисленные на основании соответствующих элементарных формул, в зависимости от температуры (давление взято за 101,325 КПа)

1.2. Влияние влажности воздуха

Под влажностью понимается наличие в воздухе газообразного водяного пара, парциальное давление которого не превосходит давления насыщенного пара для данных атмосферных условий. Добавление водяного пара в воздух приводит к уменьшению его плотности, что объясняется более низкой молярной массой воды (18 гр ⁄ мол ) по сравнению с молярной массой сухого воздуха (29 гр ⁄ мол ). Влажный воздух может рассматриваться как смесь идеальных газов, комбинация плотностей каждого из которых позволяет получить требуемое значение для их смеси. Подобная интерпретация позволяет определение значения плотности с уровнем ошибки менее 0,2% в диапазоне температур от −10 °C до 50 °C и может быть выражена следующим образом:

где — плотность влажного воздуха ( кг ⁄ м³ ); p d — парциальное давление сухого воздуха (Па); R d — универсальная газовая постоянная для сухого воздуха (287,058 Дж ⁄ (кг·К) ); T — температура (K); p v — давление водяного пара (Па) и R v — универсальная постоянная для пара (461,495 Дж ⁄ (кг·К) ). Давление водяного пара может быть определено исходя из относительной влажности:

где p v — давление водяного пара; φ — относительная влажность и p sat — парциальное давление насыщенного пара, последнее может быть представлено в виде следующего упрощенного выражения:

которое дает результат в миллибарах. Давление сухого воздуха p d определяется простой разницей:

где p обозначает абсолютное давление рассматриваемой системы.

1.3. Влияние высоты над уровнем моря в тропосфере

Зависимость давления, температуры и плотности воздуха от высоты по сравнению со стандартной атмосферой (p 0 =101325 Па, T 0 =288,15 K, ρ 0 =1,225 кг/м³).

Для вычисления плотности воздуха на определенной высоте в тропосфере могут использоваться следующие параметры (в параметрах атмосферы указано значение для стандартной атмосферы):

стандартное атмосферное давление на уровне моря — p 0 = 101325 Па;
стандартная температура на уровне моря — T 0 = 288,15 K;
ускорение свободного падения над поверхностью Земли — g = 9,80665 м ⁄ сек 2 (при данных вычислениях считается независимой от высоты величиной);
скорость падения температуры (англ.) русск. с высотой, в пределах тропосферы — L = 0,0065 K ⁄ м ;
универсальная газовая постоянная — R = 8,31447 Дж ⁄ (Мол·K) ;
молярная масса сухого воздуха — M = 0,0289644 кг ⁄ Мол .

Для тропосферы (т.е. области линейного убывания температуры — это единственное свойство тропосферы, используемое здесь) температура на высоте h над уровнем моря может быть задана формулой:

Давление на высоте h :

Тогда плотность может быть вычислена подстановкой соответствующих данной высоте h температуры T и давления P в формулу:

Эти три формулы (зависимость температуры, давления и плотности от высоты) и использованы для построения графиков, приведенных справа. Графики нормализованы — показывают обший вид поведения параметров. «Нулевые» значения для верных вычислений нужно каждый раз подставлять в соответствии с показаниями соответствующих приборов (градусника и барометра) на данный момент на уровне моря.

Зависимость плотности газа от давления график

Плотность газов

Газы в отличие от жидкостей характеризуются малой плотностью. Нормальной плотностью газа называется масса одного его литра при 0°С и давлении 1 кгс/см2. Масса одной молекулы любого газа пропорциональна его плотности.

Плотность газа с изменяется пропорционально давлению и измеряется отношением массы газа m к занимаемому им объему V:

Для практических целей различные газы удобно характеризовать по их плотности относительно воздуха при одинаковых условиях давления и температуры. Поскольку молекулы разных газов имеют различную массу, их плотности при одинаковом давлении пропорциональны молярным массам.

Плотность газов и отношение их плотности к плотности воздуха:

Плотность с, кг/м3

отношению к воздуху

Основные газовые законы

Характерным для газов является то, что они не имеют своего объема и формы, а принимают форму и занимают объем того сосуда, в который их помещают. Газы равномерно наполняют объем сосуда, стремясь расшириться и занять возможно больший объем. Все газы обладают большой сжимаемостью. Молекулы реальных газов обладают объемом и имеют силы взаимного притяжения, хотя эти величины весьма незначительны. В расчетах по реальным газам обычно используют газовые законы для идеальных газов. Идеальные газы — это условные газы, молекулы которых не имеют объема и не взаимодействуют друг с другом из-за отсутствия сил притяжения, а при столкновениях между ними не действуют никакие другие силы, кроме сил упругого удара. Эти газы строго следуют законам Бойля — Мариотта, Гей-Люссака и др.

Чем выше температура и меньше давление, тем поведение реальных газов ближе соответствует идеальным газам. При малых давлениях все газы можно рассматривать как идеальные. При давлениях около 100 кг/см2 отклонения реальных газов от законов идеальных газов не превышают 5 %. Поскольку отклонения реальных газов от законов, выведенных для идеальных газов, обычно ничтожны, законами для идеальных газов можно свободно пользоваться для решения многих практических задач.

Закон Бойля — Мариотта

Измерения объема газа под влиянием внешнего давления показали, что между объемом V и давлением Р имеется простая связь, выражающаяся законом Бойля — Мариотта: давление данной массы (или количества) газа при постоянной температуре обратно пропорционально объему газа:

где Р1 — давление газа при объеме V1; Р2 — давление газа при объеме V2.

Р1 * V1 = P2* V2 или Р * V= const (при t = const).

Этот постулат формулируется так: произведение давления данной массы газа на его объем постоянно, если температура не меняется (т.е. при изотермическом процессе).

Если, например, взять 8 л газа под давлением Р = 0,5 кгс/см2 и менять давление при неизменной постоянной температуре, то будут получены следующие данные: при 1 кгс/см2 газ займет объем 4 л, при 2 кгс/см2 — 2л, при 4 кгс/см2 — 1л; при 8 кгс/см2 — 0,5л.

Таким образом, при постоянной температуре всякое повышение давления приводит к уменьшению объема газа, а уменьшение объема газа — к повышению давления.

Зависимость между объемом газа и давлением при неизменной температуре широко применяется для различных расчетов в водолазной практике.

Законы Гей-Люссака и Шарля

Закон Гей-Люссака выражает зависимость объема и давления газа от температуры: при постоян-ном давлении объем данной массы газа прямо пропорционален его абсолютной температуре:

где Т1 и Т2 — температура в Кельвинах (К), которая равна температуре в °С + 273,15; т.е. 0°С ? 273 К; 100 °С — -373 К, а 0оК = -273,15 оС.

Следовательно, всякое повышение температуры приводит к увеличению объема, или, иными словами, изменение объема данной массы газа V прямо пропорционально изменению температуры t газа при постоянном давлении (т.е. при изобарическом процессе). Это положение выражается формулой:

где V1 — объем газа при данной температуре; V0 — исходный объем газа при 0°С; б — коэффициент объемного расширения газа.

При нагревании различных газов на одинаковое число градусов относительное приращение объема одинаково для всех газов. Коэффициент б является постоянной для всех газов величиной приращения объема, равной 1/273 или 0,00367 оС-1. Этот коэффициент объёмного расширения газов показывает, на какую часть объема, занимаемого при 0°С, возрастает объем газа, если его нагреть на 1°С при постоянном давлении.

Соотношение между давлением и температурой подчиняется той же закономерности, а именно: изменение давления данной массы газа прямо пропорционально температуре при неизменном объеме (т.е. при изохорном процессе: от греческих слов «изос» — равный и «хорема» — вместимость), что выражается формулой:

где Рt — давление газа при данной температуре; Р0 — исходное давление газа при 0° С; б — коэффициент объемного расширения газа.

Эта зависимость была установлена Ж.Шарлем за 25 лет до публикации Ж.Л.Гей-Люссака и нередко называется законом Шарля. Зависимость объема от температуры при постоянном давлении также была впервые установлена Шарлем.

При понижении температуры газа его давление убывает, а при температуре -273,15 °С давление любого газа равно нулю. Эта температура называется абсолютным нулем температуры. При этом прекращается хаотическое тепловое движение молекул и количество тепловой энергии становится равным нулю. Приведенные зависимости, выражающие законы Шарля и Гей-Люссака, позволяют решать важные практические задачи при подготовке и планировании подводных погружений, такие, например, как определение давления воздуха в баллонах при изменении температуры, соответствующие ему изменение запасов воздуха и времени пребывания на данной глубине и т. п.

Уравнение состояния идеального газа

Если зависимость между объемом, давлением и температурой связать воедино и выразить одним уравнением, то получается уравнение состояния идеального газа, которое объединяет законы Бойля — Мариотта и Гей-Люссака. Это уравнение впервые было выведено Б.П.Клайпероном путем преобразований уравнений, предложенных его предшественниками. Уравнение Клайперона состоит в том, что произведение давления газа данной массы на объем, деленное на абсолютную температуру, есть величина постоянная, не зависящая от состояния, в котором находится газ. Одна из форм написания этого уравнения:

В этом случае газовая постоянная r будет зависеть от природы газа. Если массой газа является моль (грамм-молекула), то газовая постоянная R является универсальной и не зависит от природы газа. Для массы газа, равной 1 молю, уравнение примет следующий вид:

Точное значение R cocтaвляeт 8,314510 Дж • моль -1 • К-1

Если брать не 1 моль, а любое количество газа, имеющего массу m, то состояние идеального газа можно выразить удобным для расчетов уравнением Менделеева — Клайперона в том виде, в котором оно было впервые записано Д.И.Менделеевым в 1874 г.:

где m — масса газа, г; М — молярная масса.

Уравнение состояния идеального газа может использоваться для расчетов в водолазной практике.

Пример. Определить, какой объем занимают 2,3 кг водорода при температуре + 10 °С и давлении 125 кгс/см2

где 2300 — масса газа, г; 0,082 — газовая постоянная; 283 — температура Т (273+10); 2 — молярная масса водорода М. Из уравнения следует, что давление, оказываемое газом на стенки сосуда, равно:

Это давление исчезает или при m > 0 (когда почти исчезает газ), или при V> ? (когда газ неограниченно расширяется), или при Т > 0 (когда молекулы газа не движутся).

Уравнение Ван-дер- Ваалъса

Еще М. В Ломоносов указывал на то, что закон Бойля — Мариотта не может быть верен при очень больших величинах давления, когда расстояния между молекулами сравнимы с их собственными размерами. Впоследствии полностью подтвердилось то, что отступления от поведения идеальных газов будут значительны при очень высоких давлениях и очень низких температурах. В этом случае уравнение идеального газа даст неверные результаты без учета сил взаимодействия молекул газа и занимаемого ими объема. Поэтому в 1873 г. Ян Дидерик Ван-дер-Ваальс предложил внести в это уравнение две поправки: на давление и на объем.

Авогадро выдвинул гипотезу, по которой при одинаковых условиях температуры и давления все идеальные газы независимо от их химической природы содержат в единице объема равное число молекул. Отсюда следует, что масса равных объемов газа пропорциональна их молекулярной массе.

Исходя из закона Авогадро, зная объемы исследуемых газов, можно определить их массу и, наоборот, по массе газа узнать его объем.

Законы газовой динамики

Закон Дальтона. Давление смеси газов равно сумме парциальных (частичных) давлений отдельных газов, составляющих смесь, т. е. тех давлений, которые производил бы каждый газ в отдельности, если бы он был взят при той же температуре в объеме смеси.

Парциальное давление газа Pr пропорционально процентному содержанию С данного газа и величине абсолютного давления Рабс газовой смеси и определяется по формуле:

где Pr — парциальное давление газа в смеси, кг/см2; С — объемное содержание газа в смеси, %.

Проиллюстрировать данный закон можно, сравнив смесь газов в замкнутом объеме с набором гирь различного веса, положенных на весы. Очевидно, что каждая из гирь будет оказывать давление на чашу весов независимо от наличия на ней других гирь.

Зависимость плотности газа от давления график

В данном разделе мы выведем зависимость давления газа (P) от высоты (h) над уровнем моря в гравитационном поле Земли.

Возьмем произвольную цилиндрическую колонну газа с площадью сечения (S) и высотой (h.) Вес выделенного объема газа будет равен [F = mg = rho gV = rho ghS,] где (rho) означает плотность газа. Плотность газа будет выражаться следующей формулой: [require P = frac = frac<>>> = rho gh. ] Теперь представим такую колонну в атмосфере и выделим в ней тонкий слой воздуха высотой (dh) (рисунок (1)). Ясно, что такой слой вызывает изменение давления на величину [dP = — rho gdh.] Мы поставили здесь знак минус, поскольку давление должно уменьшаться с увеличением высоты.

Рассматривая атмосферный воздух как идеальный газ, воспользуемся уравнением Менделеева-Клапейрона, чтобы выразить плотность (rho) через давление (P:) [ RT,>;; <>RT = fracRT.> ] Здесь (T) − абсолютная температура, (R) − универсальная газовая постояная, равная (8.314,>>normalsize>,) (M) − молярная масса, которая для воздуха равна (0.029,>>normalsize>.) Отсюда следует, что плотность определяется формулой [rho = frac<><>.] Подставляя это в дифференциальное соотношение для (dP,) находим: [ ><>gdh,>;; >
= — frac<><>dh.> ] В результате мы получаем дифференциальное уравнение, описывающее давление газа (P) как функцию высоты (h.) Интегрирование приводит к следующему уравнению: [ >
> = — int ><>dh> ,>;; ><>h + ln C.> ] Избавляясь от логарифмов, получаем так называемую барометрическую формулу [P = Cexp left( < - frac<><>h> right).] Константа (C) определяется из начального условия (Pleft( right) = ,) где () − это среднее атмосферное давление над уровнем моря.

Таким образом, зависимость атмосферного давления от высоты выражается формулой: [P = exp left( < - frac<><>h> right).] Подставляя известные стандартные значения (смотрите рисунок (2) выше), находим зависимость (Pleft( h right)) (в килопаскалях), которая описывается формулой [ ><<8.3143 cdot 288.15>>h> right) > = <101.325exp left( < - 0.00012,h>right);left[text <кПа>right],> ] где высота (h) над уровнем моря выражается в метрах.

Если давление определяется в миллиметрах ртутного столба (left( text <мм.рт.ст.>right),) то барометрическая формула принимает вид: [Pleft( h right) = 760exp left( < - 0.00012,h>right);left[ text <мм.рт.ст.>right].] Барометрическая формула широко используется для оценки атмосферного давления при различных условиях, хотя она дает слегка завышенные значения.

Зависимость параметров флюидов и пористой среды от давления

Выведенные дифференциальные уравнения неразрывности и движения содержат, кроме скорости фильтрации и давления, плотность флюида ρ, коэффициент пористости m, коэффициент проницаемости k (для изотропной среды) и вязкость флюида μ. Для дальнейших расчетов надо знать зависимости этих коэффициентов от давления и температуры.

При изотермическом процессе зависимость плотности однородного флюида от давления представляет собой уравнение состояния.

При установившейся фильтрации капельной жидкости можно считать ее плотность не зависящей от давления, т. е. рассматривать жидкость как несжимаемую, тогда ρ = const.

В неустановившихся процессах часто большое количество нефти можно отобрать за счет расширения ее объема при снижении давления. В этих процессах необходим учет сжимаемости жидкости. При движении газа необходимо учитывать зависимость плотности газа от давления. Поэтому в качестве основных уравнений состояния рассматривают уравнения состояния упругой жидкости, совершенного и реального газов.В дальнейшем считаем, что давление является функцией только плотности. Процессы, в которых называются баротропными. Примером баротропных процессов могут служить изотермические фильтрационные течения.

Коэффициент объемного сжатия жидкости β_ж равен отношению относительного изменения объема жидкости к изменению давления

(2.22)

Знак «-» поставлен для того, чтобы коэффициент объемного сжатия жидкости был положительной величиной. При увеличении давления (dp >0) уменьшается (dV_ж -1 ):

для различных нефтей отечественных месторождений — 7·10 -10 — 30·10 -10 ;

для пластовых вод 2,7·10 -10 — 5·10 -10 .

В формуле (2.22) перейдем от объемов к плотности; подставив для однородной жидкости

, ,

Т.к. М = const, получим: , откуда

Проинтегрируем последнее равенство от фиксированных значений р и ρ до текущих значений р и ρ соответственно:

и в результате получим , потенцируя, найдем

(2.23)

Показатель степени β_ж(р — p) обычно много меньше единицы. Поэтому принимают

При этом получаем линейную зависимость плотности упругой слабосжимаемой жидкости при небольших перепадах давления:

(2.24)

Для больших перепадов давления р — р надо использовать уравнение состояния упругой жидкости в виде (2.23).

Иногда вместо коэффициента объемного сжатия вводят модуль упругости жидкости К_ж = 1/ β_ж. Формулы (2.23) и (2.24), выраженные через модуль упругости Кж, примут следующий вид:

,

Природные газы можно считать идеальными (совершенными), если пластовые давления газовых месторождений невелики (до 6-9 МПа), и газ отбирают при депрессии до I МПа. Уравнением состояния идеального газа служит уравнение Клайперона-Менделеева:

где R — газовая постоянная для газа с молекулярной массой ¯μ, связанная с универсальной газовой постоянной R зависимостью .

Если Т = Т_пл = cosnt, а р_ат — плотность газа при атмосферном давлении р_ат и пластовой температуре Т_пл, то

(2.26)

Приравняв левые части соотношений (2.25) и (2.26), получим уравнение состояния идеального (совершенного) газа, которым будем пользоваться в дальнейшем:

(2.27)

В практике все чаще встречаются газовые месторождения с высокими пластовыми давлениями (до 40-60 МПа), которые иногда эксплуатируются с большими депрессиями (порядка 15-30 МПа). В этих условиях следует использовать уравнение состояния реального газа, которое, в отличие от уравнения (2.27), запишется в виде

где z — коэффициент, характеризующий степень отклонения состояния реального газа от закона идеальных газов (коэффициент сверхсжимаемости) и зависящий от давления и температуры z = z(p, Т). Значения коэффициента сверхсжимаемости z справочные данные (определяются по графикам Д. Брауна).

Для изотермической фильтрации реального газа зависимость плотности от давления принимает вид

(2.29)

Зависимость z(p) при постоянной температуре можно считать линейной при малых изменениях давления:

(2.30)

где z — коэффициент сверхсжимаемости при р = р;

и экспоненциальной при больших изменениях давления:

(2.31)

причем константа а_z подбирается так, чтобы кривая как можно ближе подходила к соответствующей эмпирической кривой на графиках Д. Брауна.

Используя приведенные уравнения состояния можно вычислить функцию Лейбензона для каждого случая.

Для упругой жидкости с уравнением состояния (2.23):

, (2.32)

При малых значениях и уравнением состояния (2.24) равенство (2.32) будет

(2.33)

т. е. имеем тот же вид, что и для несжимаемой жидкости.

Для совершенного газа с уравнением состояния

получаем , (2.34)

т. е. функция Лейбензона пропорциональна квадрату давления.

Для реального газа с уравнением состояния (2.39)

, (2.35)

т. е. функция Лейбензона записывается в виде интеграла.

93.79.221.197 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Связь между давлением, температурой, объемом и количеством молей газа («массой» газа). Универсальная (молярная) газовая постоянная R. Уравнение Клайперона-Менделеева = уравнение состояния идеального газа.

Связь между давлением, температурой, объемом и количеством молей газа («массой» газа). Универсальная (молярная) газовая постоянная R. Уравнение Клайперона-Менделеева = уравнение состояния идеального газа.

Ограничения практической применимости:

температуры ниже -100°C и выше температуры диссоциации / разложения

давления выше 90 бар

вакуум глубже чем 99%

Внутри диапазона точность уравнения превосходит точность обычных современных инженерных средств измерения. Для инженера важно понимать, что для всех газов возможна существенная диссоциация или разложение при повышении температуры.

в СИ R= 8,3144 Дж/(моль*К) — это основная (но не единственная) инженерная система измерений в РФ и большинстве стран Европы

в СГС R= 8,3144*10 7 эрг/(моль*К) — это основная (но не единственная) научная система измерений в мире

m-масса газа в (кг)

M-молярная масса газа кг/моль (таким образом (m/M) — число молей газа)

P-давление газа в (Па)

Т-температура газа в ( °K)

V-объем газа в м 3

Давайте решим парочку задач относительно газовых объемных и массовых расходов в предположении, что состав газа не изменяется (газ не диссоциирует) — что верно для большинства газов в указанных выше пределах применимости.

1) Доставка объемов газа одинаковой массы при одинаковом давлении но различных температурах.

Данная задача актуальна в основном, но не только, для применений и устройств, в которых напрямую измеряется объем газа.

Пусть счетчик (расходомер) в точке доставки дает объемные накопленные расходы V₁ и V₂, при температурах, соответственно, T₁ и T₂ и, пусть T₁ V₂ для одинаковых количеств газа при данных условиях. Попробуем сформулировать несколько важных на практике выводов для данного случая:

показатели объемного счетчика газа тем «весомее», чем выше давление

выгодно поставлять газ низкого давления

выгодно покупать газ высокого давления

Как с этим бороться? Необходима хотя бы простая компенсация по давлению, т.е в считающее устройство должна подаваться информация с дополнительного датчика давления.

Читать еще: Амплитуда колебаний давления