Давление струи жидкости на преграду

Давление струи жидкости

Вытекающая изнасадка струя при встрече с твердой преградой действует на нее силой давления, величина которой зависит от скорости и размеров поперечного сечения струи жидкость, формы и размеров преграды ее расположения по отношению к струе. Это используется в практике, например, для разрушения гидромониторами горных пород, в брандспойтах, в гидротурбинах и т. п.

В общем случае сила давления струи жидкости на преграду равна потерянному количеству движения, поэтому рассмотрим уравнение количества движения применительно к гидравлическим процессам.Как известно из механики, для материальной точки уравнение количества движения в проекции на некоторую ось х имеет вид

Применительно к жидкости теорема относится к массовому расходу, т. е к массе жидкости, проходящей через заданное сечение в 1 с. В этом случае приращение времени численно равно единице, и теорема представляется уравнением

(5.8)

которое читается: изменение количества движения массового расхода жидкости равно сумме всех внешних сил, действующих на поток. Рассмотрим случай встречи струи жидкости с плоской, перпендикулярной к оси струи преградой. Жидкость после столкновения с преградой растекается по ее поверхности (рис. 33, a), т. е. поток поворачивается на 90″, поэтому проекция скорости на направление ее первоначального движения уменьшается до нуля. Потерянная скорость равна ее абсолютной величине, а расход равен произведению сечения струи на скорость потока. Следовательно, сумма внешних сил есть реакция стенки, равная

(5.9)

Если принять значение расхода и скорости жидкости изнасадка согласно формулам (5.1) и (5.2), то сила давления струи на преграду

(5.10)

Для случая, когда препятствие располагается под углом к оси струн, сила давления

(5.11)

Если преграда представляет собой криволинейную поверхность (см. рис. 33, б), отклоняющую набегающую струю жидкости на 180°, то сила давления струи

(5.12)

т.е. превышает гидростатическое давление в 4 раза. Поэтому рабочие элементы гидротурбин имеют такую форму.

В случае, когда преграда движется в том же направлении, что и жидкость, то сила воздействия струи уменьшается:

(5.13)

Где u- скорость перемещения преграды.

Мощность, передаваемая струей плоской преграде,

. (5.14)

Давление струи жидкости на преграду

Практически очень важным является пример применения новой формы второго закона Ньютона для расчета сил давления на препятствия со стороны быстро текущей жидкости.

Подставьте ладонь под струю воды, вытекающую из полностью открытого водопроводного крана. Вы почувствуете довольно сильное давление струи на руку. Если вы попробуете подставить руку под струю воды, выходящую из пожарного брандспойта, то струя просто отбросит руку и может даже ее повредить (рис. 4.12).

Как возникает сила давления струи и как ее рассчитать?

Допустим, что площадь поперечного сечения струи воды, выбрасываемой из брандспойта, равна скорость воды плотность воды (рис. 4.13). Пусть струя падает на плоскую стенку по перпендикуляру. Определим силу, с которой струя будет давить на препятствие. Для этого сначала разберемся во всех процессах, которые происходят во время взаимодействия струи с препятствием.

Прежде всего заметим, что в течение каждой секунды до стенки успевают дойти и коснуться ее все те частицы воды, которые находились от стенки на расстоянии не больше чем (см. рис. 4.13). Следовательно, каждую секунду со стенкой будет взаимодействовать масса воды, заключенная в объеме, равном Так как плотность воды то эта масса будет равна Ясно, что в дальнейших расчетах необходимо учитывать то количество движения которое будет приносить к стенке именно эта масса, т. е.

После удара о стенку вода равномерно растекается во все стороны от места удара. Количество движения всей массы воды после удара будет слагаться из количеств движения частичек воды, уходящих от места удара в разные стороны.

Если какая-либо частица А уходит с некоторой скоростью и влево, то при равномерном растекании всегда найдется такая же частица В, которая с такой же по модулю скоростью будет уходить вправо (рис. 4.14). Количества движения таких частиц численно равны, но противоположны по направлению. Сумма количеств движения для этой пары частиц равна нулю. Так как для любой частицы воды после удара найдется такая парная ей частица, то можно утверждать, что полная сумма количеств движения всех частиц после растекания будет также равна нулю.

Другими словами, мы должны считать, что после удара о стенку полное количество движения воды становится равным нулю.

Таким образом, мы теперь знаем количество движения, которое имеет вода до взаимодействия со стенкой и после него. По известному изменению количества движения рассчитаем импульс, получаемый водой от стенки за одну секунду. По второму закону Ньютона:

Подставляя значения получим

Импульс, получаемый стенкой за ту же секунду, равен

Читать еще: Давление воронеж сейчас

(Знак в правой части уравнения изменился потому, что сила, действующая на стенку, направлена противоположно силе, действующей на воду.)

В § 77 отмечалось, что импульс силы за единицу времени численно равен самой силе. Учитывая это, запишем выражение для модуля силы, действующей на стенку со стороны струи воды:

Полученное выражение для силы действия струи воды на препятствие имеет очень важное значение.

Прежде всего обратим внимание на то, что эта сила очень быстро возрастает с увеличением скорости жидкости. Пользуясь полученной формулой, нетрудно рассчитать, например, что при скорости струя будет давить на каждый квадратный метр поверхности препятствия с силой (или При увеличении скорости до 20 м/с эти силы возрастают до т. е. при возрастании скорости только в 20 раз силы увеличились в 400 раз

Такая особенность действия быстротекущих вод явилась причиной многих природных явлений. Громадные овраги, русла и долины рек образовались благодаря разрушающему действию таких сил, создаваемых паводковыми водами. Размыв морских и озерных берегов производится такими же силами, возникающими при прибое. Эти же силы позволяют рекам транспортировать размытый ими грунт на большие расстояния. Об объеме работы, выполняемой реками с помощью этих сил, можно судить хотя бы по тому, что, например, количество взвешенных наносов, ежегодно переносимых Амударьей, равно 570 млн.

Отмеченные нами особенности обеспечили широкое использование этих сил в народном хозяйстве и промышленности. Приведем два наиболее часто встречающихся способа применения этих сил: в гидромониторах и турбинах.

Научная электронная библиотека

5.6 Динамика воздействия гидравлической струи на неподвижную преграду

В основу вывода динамических свойств струи положена теорема о количестве движения. Рассмотрим общий случай удара струи о неподвижную преграду.

Пусть в сечении 1-1 (рисунок 5.8) струя имеет площадь живого сечения w и среднюю скорость потока u. При встрече с преградой струя разделится на две части с характеристиками w₁u₁ и w₂u₂. Используя теорему о количестве движения, можно записать

(5.37)

где Rdt – импульс силы, реакция стенки.

Реакция R равна силе удара струи, то есть можно написать – R = F.

Если a₁ = a₂ = 90°, то уравнение (5.37) можно записать

Рисунок 5.8 Схема растекания струи

С учетом значения m из уравнения (5.37) получим выражение для определения силы удара струи о преграду

Разделив уравнение (5.38) на w, полученную величину F/w можно представить как динамическое давление на единицу площади струи. Это давление равно удвоенному скоростному напору.

Статическое давление струи Р_ст = r g w H, где Н – напор над центром тяжести отверстия, из которого истекает струя.

Динамическое давление струи Р_дин = g/g w u 2 = g/g w 2 g H = 2 g w H, т.е. динамическое давление в 2 раза больше статического.

Если пластина перемещается со скоростью u 2 . (5.38a)

Если помещенная в струю пластина (диск) имеет ограниченные размеры, то силу давления на неподвижный диск можно определить по формуле [44]
(5.39)

u – средняя скорость на уровне пластины.

Выражение в квадратных скобках представляет собой корректив, учитывающий соотношение d_п и d_с

При значении и d_п/d_с = 2,22, следовательно когда d_п > d_с. в 2,22 раза, силу давления на нее можно определить так же, как при набегании струи на неограниченную плоскость.

Исследования Конопкина Б.К. [44] позволяют сделать вывод, что если d_п/d_с изменяется в пределах от 0 до 2,22, то силу давления можно определить по формуле (5.40), если d_n/d_c > 2,2 силу давления можно определять, как при набегании струи на пластину неограниченных размеров.

Силу удара струи можно определить по формуле профессора Никонова Г.Н. [45]

l – расстояние от среза сопла до рассматриваемого сечения;

u – выходная скорость потока из сопла;

w – площадь сопла.

Более сложным представляются процесс изучения динамического воздействия струи на перемещающееся в ней тело.

Определим силу давления затопленной гидравлической струи на пластину (диск), перемещающуюся в возбужденном потоке (рисунок 5.9).

Силу давления струи на плоский диск можно определить, воспользовавшись известной в гидромеханике формулой сопротивления воды движению тел

F = c W r (5.40)

где с – коэффициент сопротивления;

u – скорость движения тела или скорость набегающего потока жидкости.

Рисунок 5.9 Схема растекания струи

Для определения скорости в заданной точке сечения возбужденного потока u(x, r), удаленной на расстоянии L от насадка ускорителя, воспользуемся формулой Альбертсона [36, 42]
(5.41)

где u – скорость истечения жидкости из насадка ускорителя;

К – опытный коэффициент, К = 6,4.

Подставляя значение скорости (5.41) в формулу (5.40) для определения силы давления струи на диск диаметром d, расположенном на расстояниих = l от насадка, получим

(5.42)

Принимая exp @ 1 + x, формулу (5.42) можно представить следующим образом:

(5.43)

Таким образом, по формулам (5.42) и (5.43) может быть определена сила давления струи на диск, помещенный в возбужденный поток, а по формуле (5.40) величина сопротивления воды движению этого диска.

Зная R и F, можно установить закономерность движения диска в водном потоке, воспользовавшись уравнением движения тела в водном потоке

С учетом полученных значений F и R запишем

Введем обозначения в это уравнение

(5.44)

Полученное дифференциальное уравнение движения тела в возбужденном потоке не имеет точного решения. Кроме того, в уравнении (5.44) не учитывается толщина диска, т.е. изменение скорости возбужденного потока вдоль тела (диска).

Воспользовавшись методом численного интегрирования, можно проследить качественную характеристику изучаемого процесса на некоторых частных случаях. На графиках (рисунок 5.10) приведены результаты расчетов по определению скорости движения диска на различном расстоянии от среза насадка.

График 1 показывает, что при достаточном большом расстоянии от насадка скорость тела резко уменьшается с увеличением расстояния, а затем постепенно затухает.

На графике 2 видно, что если начальное расстояние диска от насадка уменьшить (при неизменных остальных параметрах), то наблюдается резкий скачек скорости, а затем плавное убывание, как и в первом случае.

Графики 3 – 8, построенные для различных сочетаний скорости истечения потока из насадка, размеров диска, показывают на наличие прыжка скорости на начальном участке и постепенное плавное ее гашение.

К сожалению, до настоящего времени приведено мало исследований, изучающих закономерности движения лесосплавных единиц в водном потоке, возбужденном затопленной гидравлической струей.

Укажем на исследование профессора В.П. Корпачева [46], в котором приведена приближенная формула для определения скорости движения пучка в сечении, удаленном на расстоянии L от насадка

(5.45)

где u_п – скорость движения пучка в рассматриваем сечении, м/с;

U – скорость потока на выходе из насадка диаметром d;

К 0 – опытный коэффициент, зависящий от объема пучка и способа его установки относительно оси потока, определяется по графику (рисунок 5.11).

Рисунок 5.11 Значение коэффициента К 0

Diplom Consult.ru

5.3. Гидравлические струи жидкости. Структура гидравлической струи. Дальность полета струй

Поток жидкости, не ограниченный твердыми стенками, называется струей жидкости. К гидравлическим струям относят пожарные, фонтанные, гидромониторные, дождевальные и др.

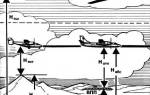
Вылетая из специального насадка при очень больших скоростях и давлениях, гидравлическая струя имеет свою определенную структуру. Это конус с двумя образующими, которые пересекаются в точке О (рис. 5.3), называемой полюсом. Сечение /—/, совпадающее с выходным сечением насадка, называется начальным

Рис. 5.3.

сечением. У начального сечения /—/ скорости по сечению струн почти одинаковые, но на расстоянии L (в сечении //—//) область одинаковых скоростей вырождается и вся толща струи становится занятой пограничным слоем с типичным распределением скоростей для однородного потока. Сечение //—//называется переходным. Участок длиной L между сечениями /—/ и //—// называется начальным. Согласно исследованиям А. Я. Миловича, скорость на начальном участке L определяется по формуле

где d — диаметр выходного отверстия насадка;  — скорость струн у выхода.

Длина начального участка L определяется по формуле L = 145 d.

Для определения дальности полета струи, при которой она не распадается, А.М. Царевский предложил следующую зависимость:

где L_c —расстояние от насадка до центра падения наиболее мощного потока струи,

м ; Н — давление на вылете струи из насадка, кПа; d — диаметр выходного отверстия насадка, м;  — угол наклона струи к горизонту, град.

Формула (1.99) справедлива для насадков диаметром до 50 мм и давлении до 0,80 МПа при угле наклона струи к горизонту 32°.

5.4. Давление струи на твердую преграду

Основной задачей при рассмотрении взаимодействия струи с различными твердыми преградами является определение давления струи на эти преграды. С этой целью Бернулли использовал теорему о равенстве

изменения количества движения импульсу действующей силы (закон изменения количества движения). Рассмотрим метод на примере взаимодействия струи с

Рис. 5.4.

выпуклой изогнутой пластиной (рис. 5.4, а)

струя отклоняется от своего первоначального направления на угол а.

Вследствие удара струи пластинка будет испытывать давление Р в направлении оси насадка S-S.

Для определения величины давления Р выделим из струи объем жидкости, прилегающий к пластинке и заключенный между сечениями 0—0, 1—1 и 1’—1′, и применим к нему закон об изменении количества движения. Изменение количества движения за время t; в рассматриваемом объеме жидкости будет равно разности количества движения массы жидкости т, имеющей скорость с и вошедшей за время t через сечение —0, и массы жидкости т, вышедшей за время t через сечение /—/ и /’—/’ из данного объема со скоростью с_.

Рис. 5.5.

Примем за ось проекций ось насадка S-S.

Спроектировав на эту ось изменение количества движения за время t, которое должно быть равно проекции импульса силы за то же время,

Получим уравнение: _mc__t_-m/2_c _cos _ __t_–_m_/2 _с_cos_ __t₌_P__t_.

Принимая с = с (потерями энергии на участке потока жидкости — и /—/ можно пренебречь), получаем

Принимая с = с (потерями энергии на участке потока жидкости — и /—/ можно пренебречь), получаем:

Pt = mc (1 — cos ) t.

Сократив обе части равенства на t, заменив т на Q, получим формулу, по которой определяется величина давления струи на пластинку:

где Q — расход насадка.

Если пластинка вогнутая, как показано на рис. 5.5, б, то угол  будет больше 90°, так как косинус тупого угла имеет отрицательное значение, т. е. второй член в скобках формулы (5.9) будет положительным. Таким образом, давление на поверхность вогнутой пластинки будет больше, чем на выпуклую пластинку.

В частном случае, когда угол  = 90° (рис. 60), величина давления Р определяется

Если вместо пластинки установить лопатку, представляющую собой два полушария (рис. 5.6), соединенных острой пластинкой, то острая пластинка будет разрезать, как ножом, струю на две равные части, из которых каждая обтекает свое полушарие. Угол в данном случае равен 180°. В связи с этим давление на неподвижную лопатку

т. e . в два раза больше, чем на плоскую пластинку.

Пример решения задач

Пример 5.1. Определить, какой напор необходимо создать в открытом резер-

вуаре диаметром d_о = 0, 5 м, чтобы из отверстия диаметром d_о = 0, 05 м, расположен-

ного в центре дна резервуара, вытекла струя с расходом Q = 5 ∙ 10 – 3 м³/с.

Дано: Решение:

d_о = 0, 5 м Истечение жидкости будет происходить при

d_о = 0, 05 м полном совершенном сжатии струи, так как

Коэффициент расхода отверстия μ = 0, 62 (см. рис.),

тогда необходимый напор

Н — ? Н = .

Пример 5.2. Определить объемный расход и скорость истечения воды из

отверстия диаметром d_о = 2, 5 ∙ 10 – 2 м в боковой стенке резервуара больших размеров.

К отверстию присоединена короткая трубка одинакового с отверстием диаметра дли-

ной l = 0, 1 м. Напор над центром отверстия Н = 1, 5 м.

Дано: Решение:

d_о = 2, 5 ∙ 10 – 2 м Длина трубки l = 4d_о, т.е. трубку можно

l = 0, 1 м рассматривать как внешний цилиндрический

Н = 1, 5 м насадок, для которого при больших числах

Рейнольдса μ = φ = 0, 8.

Скорость истечения воды находим по

υ — ? = ;

расход определяем по формуле:

Q = μω_o = 0, 8 = 2, 13 ∙ 10 -3 м³/с.

ГИДРОДИНАМИЧЕСКОЕ ДАВЛЕНИЕ СТРУИ ЖИДКОСТИ НА СТЕНКУ

Практический интерес, в частности при расчетах распределителей типа сопло-заслонка, может представить величина силы давления потока жидкости на стенку, расположенную перпендикулярно или под углом к направлению потока (рис. 28, а).

Реакция струи жидкости на стенку в заданном направления измеряется проекцией на это направление изменения количества движения. В общем случае воздействие струи на стенку определится разностью секундных количеств движения на входе и выходе. В случае плоской и неподвижной стенки диаметром больше шести диаметров сечения струи и расположенной перпендикулярно к направлению потока расчетное усилие его реакции на стенку для установившегося движения жидкости будет равно секундному импульсу силы (без учета сопротивления воздуха):

где m и Q – масса и секундный расход жидкости;

u – средняя скорость потока жидкости;

γ – объемный вес.

Принимая во внимание, что Q = , можем написать

где ρ – плотность жидкости;

ω – поперечное сечение потока.

Рис. 28. Схемы действия струи жидкости на стенки

Если стенка перемещается в том или ином направлении со скоростью ± V, то скорость встречи струи со стенкой уменьшится в отношении при перемещении стенки в том же направлении, что и направление набегающей струи, и увеличится в отношении при перемещении ее в противоположном направлении. В соответствии с этим для перпендикулярного расположения стенки (см. рис. 28, а) будем иметь

Фактическое усилие зависит от расстояния х между срезом сопла и стенкой. При увеличении этого расстояния сила давления уменьшается, поскольку при удалении сопла от преграды растет площадь круга рассеивания и уменьшается давление в центре этого круга.

При неподвижной установке плоской стенки под углом 0 к направлению потока (рис. 28, б) это усилие будет

Для случая воздействия струи на криволинейную (круглую) пластину (полусферу) сравнительно небольших размеров (принимаем скорость обтекания равной скорости у входа из сопла) рассматриваемое усилие будет (рис. 28, в)

Если угол α становится тупым (рис. 28, г), равным 180- α₁, будем иметь

С увеличением угла α давление струи на стенку возрастет, достигая при полном повороте струи (α₁ = 180 0 и α = 0) значения