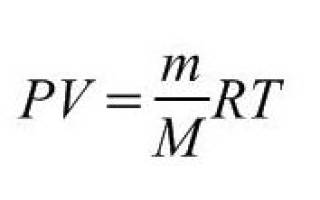Давление умноженное на объем

Связь между давлением, температурой, объемом и количеством молей газа («массой» газа). Универсальная (молярная) газовая постоянная R. Уравнение Клайперона-Менделеева = уравнение состояния идеального газа.

Связь между давлением, температурой, объемом и количеством молей газа («массой» газа). Универсальная (молярная) газовая постоянная R. Уравнение Клайперона-Менделеева = уравнение состояния идеального газа.

Ограничения практической применимости:

• температуры ниже -100°C и выше температуры диссоциации / разложения
• давления выше 90 бар
• вакуум глубже чем 99%

Внутри диапазона точность уравнения превосходит точность обычных современных инженерных средств измерения. Для инженера важно понимать, что для всех газов возможна существенная диссоциация или разложение при повышении температуры.

• в СИ R= 8,3144 Дж/(моль*К) — это основная (но не единственная) инженерная система измерений в РФ и большинстве стран Европы
• в СГС R= 8,3144*10 7 эрг/(моль*К) — это основная (но не единственная) научная система измерений в мире
• m-масса газа в (кг)
• M-молярная масса газа кг/моль (таким образом (m/M) — число молей газа)
• P-давление газа в (Па)
• Т-температура газа в ( °K)
• V-объем газа в м 3

Давайте решим парочку задач относительно газовых объемных и массовых расходов в предположении, что состав газа не изменяется (газ не диссоциирует) — что верно для большинства газов в указанных выше пределах применимости.

1) Доставка объемов газа одинаковой массы при одинаковом давлении но различных температурах.

Данная задача актуальна в основном, но не только, для применений и устройств, в которых напрямую измеряется объем газа.

Пусть счетчик (расходомер) в точке доставки дает объемные накопленные расходы V₁ и V₂, при температурах, соответственно, T₁ и T₂ и, пусть T₁ V₂ для одинаковых количеств газа при данных условиях. Попробуем сформулировать несколько важных на практике выводов для данного случая:

• показатели объемного счетчика газа тем «весомее», чем выше давление
• выгодно поставлять газ низкого давления
• выгодно покупать газ высокого давления

Как с этим бороться? Необходима хотя бы простая компенсация по давлению, т.е в считающее устройство должна подаваться информация с дополнительного датчика давления.

Калькулятор расчета объема газа по закону Бойля — Мариотта

Закон Бойля-Мариотта — один из фундаментальных законов физики и химии, который связывает изменения давления и объема газообразных веществ. При помощи нашего калькулятора легко решить простые задачи по физике или химии.

Закон Бойля-Мариотта

Изотермический газовый закон был открыт ирландским ученым Робертом Бойлем, который проводил опыты над газами под давлением. При помощи U-образной трубки и обычной ртути Бойль установил простую закономерность, что в каждый момент времени произведение давления на объем газа неизменно. Если говорить сухим математическим языком, то закон Бойля-Мариотта гласит, что при неизменной температуре произведение давления и объема постоянно:

Для сохранения постоянного соотношения величины должны изменяться в разные стороны: во сколько раз уменьшится одна величина, во столько же раз увеличится другая. Следовательно, давление и объем газа обратно пропорциональны и закон можно переписать в следующем виде:

где P1 и V1 — начальные значения давления и объема соответственно, а P2 и V2 — конечные значения.

Применение закона Бойля-Мариотта

Наилучшей иллюстрацией проявления открытого Бойлем закона является погружение пластиковой бутылки под воду. Известно, что если газ помещен в баллон, то давление на вещество будет определяться только стенками баллона. Другое дело, когда это пластичная бутылка, которая легко изменяет свою форму. На поверхности воды (давление 1 атмосфера) закрытая бутылка будет сохранять свою форму, однако при погружении на глубину 10 м на стенки сосуда будет действовать давление в 2 атмосферы, бутылка начнет сжиматься, а объем воздуха уменьшится в 2 раза. Чем глубже будет погружаться пластиковая тара, тем меньший объем будет занимать воздух внутри нее.

Это простая демонстрация действия газового закона иллюстрирует важный вывод для многих дайверов. Если на поверхности воды баллон с воздухом имеет емкость 20 л, то при погружении на глубину 30 м, воздух внутри сожмется в три раза, следовательно, воздуха для дыхания на такой глубине будет в три раза меньше, чем на поверхности.

Помимо дайверской темы, закон Бойля-Мариотта в действии можно наблюдать в процессе сжатия воздуха в компрессоре или в расширении газов при использовании насоса.

Наша программа представляет собой онлайн-инструмент, при помощи которого легко рассчитать пропорцию для любого газового изотермического процесса. Для использования инструмента вам требуется знать три любые величины, а калькулятор автоматически рассчитает искомую.

Примеры работы калькулятора

Школьная задача

Рассмотрим простую школьную задачку, в которой требуется найти первоначальный объем газа, если давление изменилось с 1 до 3 атмосфер, а объем уменьшился до 10 л. Итак, у нас есть все данные для расчета, которые требуется ввести в соответствующие ячейки калькулятора. В итоге получаем, что первоначальный объем газа составлял 30 литров.

Еще о дайвинге

Вспомним пластиковую бутыль. Представим, что мы погрузили бутыль, наполненную 19 л воздуха на глубину 40 м. Как изменится объем воздуха на поверхности? Это более сложная задачка, но только потому, что нам требуется перевести глубину в давление. Мы знаем, что на поверхности воды атмосферное давление составляет 1 бар, а при погружении в воду давление увеличивается на 1 бар каждые 10 м. Это означает, что на глубине 40 м бутыль будет под давлением приблизительно 5 атмосфер. У нас есть все данные для расчета, и в результате мы увидим, что объем воздуха на поверхности увеличится до 95 литров.

Заключение

Закон Бойля-Мариотта встречается в нашей жизни довольно часто, поэтому вам несомненно пригодится калькулятор, который автоматизирует расчеты по этой простой пропорции.

ЗАКОН БОЙЛЯ-МАРИОТТА

Научно-технический энциклопедический словарь .

Смотреть что такое «ЗАКОН БОЙЛЯ-МАРИОТТА» в других словарях:

Закон Бойля — Мариотта — Воздух (или инертный газ), находящийся в запечатанном пакете с печеньем расширяется, когда продукт поднят на значительную высоту над уровнем моря (ок 2000 м) Закон Бойля Мариотта один из основных газовых з … Википедия

Закон Бойля-Мариотта — Закон Бойля Мариотта один из основных газовых законов. Закон назван в честь ирландского физика, химика и философа Роберта Бойля (1627 1691), открывшего его в 1662, а также в честь французского физика Эдма Мариотта (1620 1684), который открыл… … Википедия

ЗАКОН БОЙЛЯ МАРИОТТА — один из основных газовых законов, согласно которому при постоянной температуре Т для данной массы m идеального (см.) произведение давления р на занимаемый им объём V есть величина постоянная: pV = const … Большая политехническая энциклопедия

закон Бойля-Мариотта — Boilio ir Marioto dėsnis statusas T sritis Standartizacija ir metrologija apibrėžtis Idealiųjų dujų dėsnis: suslėgtų dujų slėgio ir tūrio sandauga, kai temperatūra pastovi, nekinta, t. y. pV = const. Realiosioms dujoms galioja tik apytiksliai… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

закон Бойля-Мариотта — Boilio ir Marioto dėsnis statusas T sritis fizika atitikmenys: angl. Boyle and Mariotte law; Boyle Mariotte law vok. Boyle Mariottesches Gesetz, n rus. закон Бойля Мариотта, m pranc. loi de Boyle Mariotte, f … Fizikos terminų žodynas

закон Бойля-Мариотта и Гей-Люссака — Boilio, Marioto ir Gei Liusako dėsnis statusas T sritis fizika atitikmenys: angl. Boyle Charles law; Boyle Gay Lussac law vok. Boyle Charlessches Gesetz, n; Boyle Mariotte Gay Lussacsches Gesetz, n rus. закон Бойля Мариотта и Гей Люссака, m pranc … Fizikos terminų žodynas

Бойля-Мариотта закон — закон, связывающий изменения объема газа при постоянной температуре с изменениями его упругости. Этот закон, открытый в 1660 г. англ. физиком Бойлем и позже, но, независимо от него, Мариоттом во Франции, по своей простоте и определенности… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

закон бойля-маріотта — закон Бойля Мариотта Boyle’s and Mariotte’s law *Boyle Mariottesches Gesetz – закон iдеальних газiв, згiдно з яким добуток тиску на об єм незмiнної маси такого газу при сталiй температурi є величина стала: (pV) т = const. У певних межах… … Гірничий енциклопедичний словник

Бойля-Мариотта закон — Уравнение состояния Статья является частью серии «Термодинамика». Уравнение состояния идеального газа Уравнение Ван дер Ваальса Уравнение Дитеричи Разделы термодинамики Начала термодинамики Уравнен … Википедия

Бойля-Мариотта закон — Бойля Мариотта закон: произведение объёма данной массы идеального газа на его давление постоянно при постоянной температуре; установлен независимо Р. Бойлем (1662) и Э. Мариоттом (1676). * * * БОЙЛЯ МАРИОТТА ЗАКОН БОЙЛЯ МАРИОТТА ЗАКОН, один из… … Энциклопедический словарь

Закон Бойля-Мариотта. Изотерма

Первый газовый закон был открыт анг­лийским ученым Р. Бойлем в 1662 г. при исследовании упругости воздуха.

Между дав­лением и объемом данной массы газа при постоянной температуре существует обратная зависимость: p

Немного позже, в 1676 году француз­ский ученый Э. Мариотт независимо от Р. Бойля обобщенно сформулировал газо­вый закон, который теперь называют законом Бойля-Мариотта. По его утверждению, если при определенной температуре данная масса газа занимает объем V₁ при давлении p₁ , а в другом состоянии при этой же температуре его давление и объем рав­няются p₂ и V₂ , то справедливо соотно­шение:

Закон Бойля-Мариотта: если при постоянной темпе­ратуре происходит термодинамический про­цесс, вследствие которого газ переходит из одного состояния ( p₁ и V₁ ) в другое ( p₂ и V₂ ), то произведение давления на объем данной массы газа при постоянной температуре яв­ляется постоянным: pV = const .

где p — давление, V — объем, T — термодинамическая температура (изотермический процесс).

Закон Бойля-Мариотта устанав­ливает соотношение между дав­лением и объемом газа для изотермических процессов: при постоянной температуре объем V данной массы газа обратно пропорциональный его давлению P .

Термодинамический процесс, который про­исходит при постоянной температуре, на­зывается изотермическим (от гр. isos — рав­ный, therme — теплота). Графически на коор­динатной плоскости pV он изображается гиперболой, которая называется изотермой . Разным температурам отвечают разные изотермы — чем выше температура, тем выше на координатной плоскости pV находится гипербола ( T2>T1 ). Очевидно, что на координатной плоскости рТ и VT изо­термы изображаются прямыми, перпендику­лярными оси температур.

КОМПРЕССОРЫ

Закон идеального газа.

Основными параметрами газа являются температура, давление и объём. Объем газа существенно зависит от давления и температуры газа. Поэтому необходимо найти соотношение между объемом, давлением и температурой газа. Такое соотношение называется уравнением состояния.

Экспериментально было обнаружено, что для данного количества газа в хорошем приближении выполняется соотношение: при постоянной температуре объем газа обратно пропорционален приложенному к нему давлению (рис.1) :

Например, если давление, действующее на газ, увеличится вдвое, то объем уменьшится до половины первоначального. Это соотношение известно как закон Бойля (1627-1691)-Мариотта(1620-1684) , его можно записать и так:

Это означает, что при изменении одной из величин, другая также изменится, причем так, что их произведение останется постоянным.

Зависимость объема от температуры (рис.2) была открыта Ж. Гей-Люссаком. Он обнаружил, что при постоянном давлении объем данного количества газа прямо пропорционален температуре:

График этой зависимости проходит через начало координат и, соответственно, при 0К его объём станет равный нулю, что очевидно не имеет физического смысла. Это привело к предположению, что -273 0 С минимальная температура, которую можно достичь.

Третий газовый закон, известный как закон Шарля, названный в честь Жака Шарля (1746-1823). Этот закон гласит: при постоянном объеме давление газа прямо пропорционально абсолютной температуре (рис.3):

Хорошо известным примером действия этого закона является баллончик аэрозоля, который взрывается в костре. Это происходит из-за резкого повышения температуры при постоянном объеме.

Эти три закона являются экспериментальными, хорошо выполняющимися в реальных газах только до тех пор, пока давление и плотность не очень велики, а температура не слишком близка к температуре конденсации газа, поэтому слово «закон» не очень подходит к этим свойствам газов, но оно стало общепринятым.

Газовые законы Бойля-Мариотта, Шарля и Гей-Люссака можно объеденить в одно более общее соотношение между объёмом, давлением и температурой, которое справедливо для определенного количества газа:

Это показывает, что при изменении одной из величин P , V или Т, изменятся и две другие величины. Это выражение переходит в эти три закона, при принятии одной величины постоянной.

Теперь следует учесть ещё одну величину, которую до сих пор мы считали постоянной — количество этого газа. Экспериментально подтверждено, что: при постоянных температуре и давлении замкнутый объём газа увеличивается прямо пропорционально массе этого газа:

Эта зависимость связывает все основные величины газа. Если ввести в эту пропорциональность коэффициент пропорциональности, то мы получим равенство. Однако опыты показывают, что в разных газах этот коэффициент разный, поэтому вместо массы m вводят количество вещества n (число молей).