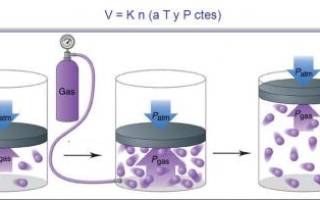
Как найти начальное давление газа

Комбинированный Закон Газа

Комбинированный Закон газа, который сочетает в себе закон Шарля, закон Бойля-Мариотта, закон Гей-Люссака.

Twitter
VK
Telegram
Skype
Email

Комбинированная формула Законов газа:

Уравнение: PiVi / Ti = PfVf / Tf

Начальный объем (Vi) = PfVfTi / TFPI
Начальное давление (Pi) = PfVfTi / TfVi
Начальная температура (Ti) = PiViTf / PfVf
Конечный объем (V) = PiViTf / TiPf
Конечное давление (Pf) = PiViTf / TiVf
Конечная температура (T) = PfVfTi / PiVi

где,

Vi = Начальный объем,
Pi = начальное давление,
Ti = начальная температура,
Vf = конечный объем,
Pf = конечное давление,
Tf = конечной температуре.

Комбинированный Закон Газа, Пример:
Пример 1: емкость содержат объем газа 30 л, при давлении 110 кПа и температуре 420 K. Найти температуру газа, которая имеет объем 40 л при давлении 120 кПа.
Vi = 30 L, P = 110 кПа, Ti = 420 K, Vf = 40 L, Р = 120 кПа
Расчет конечной температуры:
Конечная температура (T) = PfVfTi / Пиви
= (120 х 40 х 420) / (110 х 30)
= 2016000/3300
Конечная температура (T) = 610,91 K
Этот пример поможет вам рассчитать конечную температуру вручную.

Пример 2: емкость содержит объем газа 10 л, при давлении 80 кПа и температуре 200 К. Найти температуру газа, которая имеет объем 20 л при температуре 220 К.
Vi = 10 L, P = 80 кПа, Ti = 200 K, Vf = 20 L, Т = 220 кПа
Расчет давления:
Конечное давление (Pf) = PiViTf / TiVf
= (80 х 10 х 220) / (200 х 20)
= 176000/4000
Конечное давление (V) = 44 кПа
Этот пример поможет вам рассчитать давление вручную.

Калькулятор комбинированного закона газа

Комбинированный газовый закон — это формула, которая связывает основные параметры идеального газа и позволяет вычислять неизвестные в случаях, если заданы пять остальных величин.

Идеальный газ

Идеальный газ — это математическая модель с определенными допущениями, которая позволяет исследовать свойства газообразных веществ с достаточной точностью. К допущениям, которые используются в модели идеального газа, относятся:

пренебрежение размерами молекул;
силы молекулярного взаимодействия не учитываются;
соударение атомов и молекул абсолютно упруго;
газ находится в термодинамическом равновесии.

Благодаря этим допущениям ученые изучили основные свойства газообразных веществ и вывели основные законы, которым подчиняются любые газы. Комбинированный закон объединяет все перечисленные ниже зависимости.

Газовые законы

Любое газообразное вещество характеризуется тремя простыми параметрами: объемом, давлением и температурой. Газ тем и хорош, что он заполняет весь предоставленный объем или может сжиматься до минимальных объемов, иногда переходя в состояние жидкости. Сжимать газ можно двумя способами:

при постоянном давлении уменьшить температуру;
при постоянной температуре увеличить давление.

Эти две простые формулировки отражают в себе два известных газовых закона: изобару и изотерму. В изобарном процессе изменение температуры приводит к прямо пропорциональному изменению объема. Вспомните жидкий азот: он занимает минимум места, при этом его температура составляет 63,29 К, что соответствует –209 градусам Цельсия. Если температуру азота поднять до 20 градусов Цельсия, то 1 литр жидкого азота превратится в 700 литров газа. Увеличивается температура, увеличивается объем и наоборот. Эти изменения обусловлены тем, что соотношение объема к температуре газа остается статичным.

В изотермическом процессе температура не изменяется и для сжатия газа придется увеличить давление. Это процесс проще для понимания, так как сдавливая газ мы уменьшаем его объем подобно тому, как утрамбовывание грунта или снега позволяет уложить их более плотно и с меньшим объемом. В этом изотермическом процессе изменение давления приводит к обратно пропорциональному изменению объема. Больше давление, меньше объем и наоборот. Такая динамика обусловлена тем, что произведение давления на объем — это всегда постоянная величина.

Если же объем газа не изменяется, то процесс называется изохорным и в этом процессе отображается взаимосвязь давления и температуры. Согласно закону, изменение одного параметра вызывает прямо пропорциональное изменение другого. Это означает, что увеличение давления в сосуде вызывает рост температуры находящегося там газа. Верно и обратное утверждение.

Комбинированный закон

Все перечисленные законы подчиняются общей формулировке: при постоянстве одного параметра, отношение двух других также постоянно. Обобщая эти законы в динамике получаем комбинированный газовый закон, который описывается формулой:

где P1, V1 и T1 — соответственно начальные давление, объем и температура, а P2, V2 и T2 — конечные.

Используя данную формулу легко определить динамику параметров во время нагрева газа или его сжатия.

Наша программа позволяет рассчитать соотношение параметров идеального газа при их изменении. Для использования калькулятора требуется задать пять известных величин, после чего программа определит последнее неизвестное. Рассмотрим небольшой пример.

Пример использования калькулятора

Представим баллон газа объемом 15 л под давлением 120 кПа и при температуре –20 градусов Цельсия. Определим температуру газа, если баллон будет заменен на емкость объемом 10 л и давлением 150 кПа. На первый взгляд у нас есть все параметры, однако в газовых законах температура обязательно указывается в кельвинах, а не градусах. Для перевода температуры в систему Си достаточно прибавить к значению величину 273. Получаем, что температура газа составляет 253 К. Теперь вводим данные в соответствующие ячейки и смотрим на результат: конечная температура теперь равна 210 К или –63 градуса Цельсия. Очевидно, что газ подчинился приведенным выше законам и при уменьшении объема его температура также уменьшилась.

Читать еще: Высокое давление почему возникает

Заключение

Газовые законы — серьезная тема школьного курса физики, которую более подробно разбирают на первом году обучения в вузах. Комбинированный закон газа прост на первый взгляд, но обилие параметров может запутать школьника, а выведение пропорций и вовсе способно превратить задачу в ад. Для упрощения расчетов используйте наш онлайн-калькулятор, не забывая переводить все заданные параметры в систему СИ.

Давление газа — формула. Формула давления газа в сосуде

Давление является одним из трех основных термодинамических макроскопических параметров любой газовой системы. В данной статье рассмотрим формулы давления газа в приближении идеального газа и в рамках молекулярно-кинетической теории.

Идеальные газы

Каждый школьник знает, что газ является одним из четырех (включая плазму) агрегатных состояний материи, в котором частицы не имеют определенных положений и движутся хаотичным образом во всех направлениях с одинаковой вероятностью. Исходя из такого строения, газы не сохраняют ни объем, ни форму при малейшем внешнем силовом воздействии на них.

В любом газе средняя кинетическая энергия его частиц (атомов, молекул) больше, чем энергия межмолекулярного взаимодействия между ними. Кроме того, расстояния между частицами намного превышают их собственные размеры. Если молекулярными взаимодействиями и размерами частиц можно пренебречь, тогда такой газ называется идеальным.

В идеальном газе существует лишь единственный вид взаимодействия — упругие столкновения. Поскольку размер частиц пренебрежимо мал в сравнении с расстояниями между ними, то вероятность столкновений частица-частица будет низкой. Поэтому в идеальной газовой системе существуют только столкновения частиц со стенками сосуда.

Все реальные газы с хорошей точностью можно считать идеальными, если температура в них выше комнатной, и давление не сильно превышает атмосферное.

Причина возникновения давления в газах

Прежде чем записать формулы расчета давления газа, необходимо разобраться, почему оно возникает в изучаемой системе.

Согласно физическому определению, давление – это величина, равная отношению силы, которая перпендикулярно воздействует на некоторую площадку, к площади этой площадки, то есть:

Выше мы отмечали, что существует только один единственный тип взаимодействия в идеальной газовой системе – это абсолютно упругие столкновения. В результате них частицы передают количество движения Δp стенкам сосуда в течение времени соударения Δt. Для этого случая применим второй закон Ньютона:

Именно сила F приводит к появлению давления на стенки сосуда. Сама величина F от столкновения одной частицы является незначительной, однако количество частиц огромно (≈ 10 23 ), поэтому они в совокупности создают существенный эффект, который проявляется в виде наличия давления в сосуде.

Формула давления газа идеального из молекулярно-кинетической теории

При объяснении концепции идеального газа выше были озвучены основные положения молекулярно-кинетической теории (МКТ). Эта теория основывается на статистической механике. Развита она была во второй половине XIX века такими учеными, как Джеймс Максвелл и Людвиг Больцман, хотя ее основы заложил еще Бернулли в первой половине XVIII века.

Согласно статистике Максвелла-Больцмана, все частицы системы движутся с различными скоростями. При этом существует малая доля частиц, скорость которых практически равна нулю, и такая же доля частиц, имеющих огромные скорости. Если вычислить среднюю квадратичную скорость, то она примет некоторую величину, которая в течение времени остается постоянной. Средняя квадратичная скорость частиц однозначно определяет температуру газа.

Применяя приближения МКТ (невзаимодействующие безразмерные и хаотично перемещающиеся частицы), можно получить следующую формулу давления газа в сосуде:

Здесь N – количество частиц в системе, V – объем, v – средняя квадратичная скорость, m – масса одной частицы. Если все указанные величины определены, то, подставив их в единицах СИ в данное равенство, можно рассчитать давление газа в сосуде.

Формула давления из уравнения состояния

В середине 30-х годов XIX века французский инженер Эмиль Клапейрон, обобщая накопленный до него экспериментальный опыт по изучению поведения газов во время разных изопроцессов, получил уравнение, которое в настоящее время называется универсальным уравнением состояния идеального газа. Соответствующая формула имеет вид:

Здесь n – количество вещества в молях, T – температура по абсолютной шкале (в кельвинах). Величина R называется универсальной газовой постоянной, которая была введена в это уравнение русским химиком Д. И. Менделеевым, поэтому записанное выражение также называют законом Клапейрона-Менделеева.

Из уравнения выше легко получить формулу давления газа:

Равенство говорит о том, что давление линейно возрастает с температурой при постоянном объеме и увеличивается по гиперболе с уменьшением объема при постоянной температуре. Эти зависимости отражены в законах Гей-Люссака и Бойля-Мариотта.

Если сравнить это выражение с записанной выше формулой, которая следует из положений МКТ, то можно установить связь между кинетической энергией одной частицы или всей системы и абсолютной температурой.

Давление в газовой смеси

Отвечая на вопрос о том, как найти давление газа и формулы, мы ничего не говорили о том, является ли газ чистым, или речь идет о газовой смеси. В случае формулы для P, которая следует из уравнения Клапейрона, нет никакой связи с химическим составом газа, в случае же выражения для P из МКТ эта связь присутствует (параметр m). Поэтому при использовании последней формулы для смеси газов становится непонятным, какую массу частиц выбирать.

Читать еще: Как выявить причину высокого давления

Когда необходимо рассчитать давление смеси идеальных газов, следует поступать одним из двух способов:

Рассчитывать среднюю массу частиц m или, что предпочтительнее, среднее значение молярной массы M, исходя из атомных процентов каждого газа в смеси;
Воспользоваться законом Дальтона. Он гласит, что давление в системе равно сумме парциальных давлений всех ее компонентов.

Пример задачи

Известно, что средняя скорость молекул кислорода составляет 500 м/с. Необходимо определить давление в сосуде объемом 10 литров, в котором находится 2 моль молекул.

Ответ на задачу можно получить, если воспользоваться формулой для P из МКТ:

Здесь содержатся два неудобных для выполнения расчетов параметра – это m и N. Преобразуем формулу следующим образом:

Объем сосуда в кубических метрах равен 0,01 м 3 . Молярная масса молекулы кислорода M равна 0,032 кг/моль. Подставляя в формулу эти значения, а также величины скорости v и количества вещества n из условия задачи, приходим к ответу: P = 533333 Па, что соответствует давлению в 5,3 атмосферы.

Основы расчета газопроводов

Потребление газа характеризуется большой неравномерностью по месяцам года, дням, неделям и часам суток.

Режим работы системы газоснабжения зданий зависит от многих факторов: в жилых зданиях – от числа и типа установленных газовых приборов, степени благоустройства зданий, климатических условий, времени года, количества людей, проживающих в зданиях; в коммунально-бытовых, общественных и производственных зданиях, помимо перечисленных факторов – от характера работы технологического оборудования и технологических процессов, режима работы цехов и предприятия в целом.

Системы газоснабжения рассчитывают на подачу максимального расчетного часового расхода газа, который определяется по годовой потребности в газе.

Максимальный часовой расход газа на хозяйственные и производственные нужды при нормальных условиях (давлении 0,1 Мпа при 0°С) определяют по формуле

где – годовой расход газа, м 3 /год; − коэффициент перехода от годового расхода газа к максимальному часовому (коэффициент часового максимума расхода газа).

Для жилых и общественных зданий расчетный часовой расход газа определяют с учетом общего числа газовых однотипных приборов n, числа их типов или однотипных групп m, номинального расхода газ одним газовым прибором – по паспорту или технической характеристике , м 3 /ч, и коэффициенту одновременного действия приборов , по формуле

Для расчета газопроводов выполняют гидравлический расчет из условий бесперебойной подачи газа в часы максимального газопотребления.

Расчет трубопроводов газовой сети сводится к подбору диаметров труб по расчетным расходам и потерям давления газа.

Предварительное определение диаметров отдельных расчетных участков газопроводов выполняется по формуле

где − часовой расход газа, м 3 , при нормальных начальных условиях давления и температуры газа (0,1 Мпа и 0°С); − абсолютное давление газа на расчетном участке газопровода, МПа; – скорость движения газа, м/с.

Далее определяют падение давления газа по длине газопровода и в местных сопротивлениях: на поворотах, в соединениях, в фасонных частях, арматуре и пр. С учетом дополнительного гидростатического напора газа это падение давления сравнивают с допустимым. Если падение давления превышает допустимую величину, то делают перерасчет диаметров на отдельных расчетных участках в сторону их увеличения.

Падение давления газа по длине газопровода низкого давления определяют в зависимости от режима движения газа, который характеризуется числом Рейнольдса:

Для ламинарного режима движения газа при Re ≤ 2000 падение давления газа на трение по длине:

для турбулентного режима при Re > 4000

где – падение давления, Па; – расход газа, м 3 /ч, при нормальных условиях (давление 0,1 МПа и температуре 0°С); d – внутренний диаметр газопровода, см; – коэффициент кинематической вязкости газа, м 2 /с, при нормальных начальных условиях состояния газа; – плотность газа, кг/м 3 , тоже при нормальных начальных условиях состояниях газа; – эквивалентная абсолютная шероховатость труб: для стальных труб = 0,01, полиэтиленовых = 0,005; – расчетная длина участка газопровода одного диаметра, см.

Для внутренних и наружных газопроводов расчетную длину определяют с учетом приведенной длины, зависящей от эквивалента длины трубы, учитывающей местные сопротивления:

где – расчетная длина газопровода, м; – действительная длина газопровода, м; − приведенная длина газопровода, м, равная:

– эквивалентная длина, на которой падение давления газа на трение равно падению давления в местных сопротивлениях при = 1; ∑ζ – сумма коэффициентов местных сопротивлений на расчетном участке газопровода длиной .

Эквивалентную длину определяют по формулам:

для ламинарного режима движения газа

для турбулентного режима движения газа

0,25

Для жилых домов в газопроводах низкого давления местные потери давления газа определяют как часть от потерь по длине, т.е. линейных потерь, %:

на внутриквартирной разводке в зависимости от длины, %:

до 2 м………………450 до 7 м…………………120

Допустимую величину потерь давления принимают:

во внутренних и дворовых газопроводах……………60 даПа (60 мм)

в уличных и внутриквартальных газопроводах…….120 даПа (120 мм)

Таким образом, общая допустимая потеря давления в распределительных сетях низкого давления (от ГРП до самого отдаленного потребителя газа) составляет 180 даПа.

Читать еще: Если всегда пульс 90

При гидравлическом расчете газопроводной сети здания необходимо учитывать естественный гидростатический напор газа, возникающий в связи с тем, что плотность газа меньше плотности воздуха, и как результат газ поднимается вверх по газопроводу.

Гидростатический напор, Па, определяют по формуле

где – высота подъема газа, т.е. разность геодезических отметок начального и

конечного участка газопровода, м;

и – плотность воздуха и газа, кг/м 3 , при нормальных начальных условиях

состояния газа (давлении 0,1 МПа и температуре 0°С).

В результате гидравлического расчета следует проверить условие обеспечения подачи газа потребителям, т.е. чтобы давление газа на вводе было не меньше требуемого давления с учетом гидростатического напора :

Величина требуемого давления равна:

где – необходимое давление газа у диктующего газового прибора, Па или даПа; − гидростатический напор, Па;

∑ – сумма потерь давления по длине и в местных сопротивлениях в сети от ввода до диктующего газового прибора, Па.

Если неравенство не выполняется, то следует увеличить диаметры труб, с тем чтобы уменьшить общие потери давления.

Для нормальной работы бытовых газовых приборов всегда указывается номинальное давление газа 2 (200 мм) или 1,3 кПа (130 мм), поэтому после ГРП в газовой сети устанавливают давление газа соответственно 3 (300 мм) или 2 кПа (200 мм).

Таким образом, при расчете газовых сетей в зданиях необходимо учитывать следующие условия:

1. На вводе создается располагаемое давление газа , равное действующему (фактическому) давлению плюс дополнительное естественное давление газа (гидростатический напор), т.е.

2. Располагаемое давление всегда должно быть не меньше требуемого:

3. Требуемое давление складывается из потерь по длине и в местных сопротивлениях и номинального давления у газовых приборов без естественного гидростатического напора.

4. Расчет газовой сети следует выполнять правильно, чтобы сумма допустимых потерь давления в газовых сетях не была бы меньше фактических потерь:

Допустимая величина потерь давления в газовых сетях приведена

Давление идеального газа

Общие понятия о давлении идеального газа

Молекулы в идеальном газе совершают движения, при этом они ударяются о стенки сосуда, в котором газ находится, создавая этим давление газа на стенки. Это давление (p) легко вычисляется исходя из представлений молекулярно-кинетической теории (МКТ). Для облегчения данной задачи вводят следующие упрощения:

Так как давление газа не зависит от формы сосуда, в котором этот газ находится, поэтому будем считать, что сосуд имеет форму прямоугольного параллелепипеда, стороны которого .
Пусть сталкивающиеся со стенкой молекулы газа испытывают зеркальное отражение от нее, без изменения величины скорости, взаимодействуют со стеной по закону абсолютно упругого удара.
Все направления движения молекул следует считать равновероятными, если газ находится в равновесии. Для упрощения считаем, что молекулы движутся только в трех взаимно перпендикулярных направлениях, которые совпадают с ребрами параллелепипеда. Тогда, если в сосуде находится N молекул, то в каждом направлении движется молекул (вдоль одного ребра ).

Вычисление давления идеального газа

Выделим на стенке сосуда маленькую площадку , определим каково давление, которое газ оказывает на нее.

При соударении молекула, которая движется по нормали к площадке, передает ей импульс равный:

где – масса молекулы, v – скорость молекулы. За время равное выделенной площадки достигают только те молекулы, которые находятся в объеме цилиндра основание которого равно , а высота: . Количество таких молекул равно , где n – число молекул в единице объема газа. На самом деле молекулы движутся к выделенной площади под разными углами и имеют разные скорости, и скорость молекулы при каждом соударении со стенкой изменяется. Тогда принимая во внимание пункт 3 сделанных нами допусков имеем, что число ударов молекул о площадку будет равно: . Импульс, который получает стенка при ударах этого числа молекул, равен:

В таком случае давление газа на стенку получается равно:

Определим среднеквадратичную скорость (), которая характеризует всю совокупность молекул газа, как:

где N – число молекул в объема газа равном V. Тогда давление идеального газа равно:

Уравнение (5) называют основным уравнением МКТ. Приведенный вывод формулы (5) является очень приблизительным, но точный расчет давления с учетом движения молекул по всем направлениям даст такую же формулу.

Основное уравнение МКТ часто записывают в виде:

где – средняя кинетическая энергия поступательного перемещения молекул газа.

Давление идеального газа можно вычислить, применяя уравнения состояния:

где T – температура газа по абсолютной шкале температур (в К).

или уравнение состояния, называемое уравнением Менделеева — Клапейрона

где – молярная масса газа; R- универсальная газовая постоянная.

Примеры решения задач

Массу одной молекулы газа можно вычислить, применяя известное соотношение:

где m – масса газа; – молярная масса газа; N – число молекул газа в данной массе m; – число Авогадро. Если мы хотим вычислить массу одной молекулы, то положим , из (1.2) имеем: