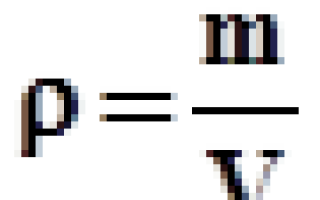Зависимость плотности природного газа от давления и температуры

Зависимость плотности природного газа от давления и температуры

Плотность газов

Газы в отличие от жидкостей характеризуются малой плотностью. Нормальной плотностью газа называется масса одного его литра при 0°С и давлении 1 кгс/см2. Масса одной молекулы любого газа пропорциональна его плотности.

Плотность газа с изменяется пропорционально давлению и измеряется отношением массы газа m к занимаемому им объему V:

Для практических целей различные газы удобно характеризовать по их плотности относительно воздуха при одинаковых условиях давления и температуры. Поскольку молекулы разных газов имеют различную массу, их плотности при одинаковом давлении пропорциональны молярным массам.

Плотность газов и отношение их плотности к плотности воздуха:

Плотность с, кг/м3

отношению к воздуху

Основные газовые законы

Характерным для газов является то, что они не имеют своего объема и формы, а принимают форму и занимают объем того сосуда, в который их помещают. Газы равномерно наполняют объем сосуда, стремясь расшириться и занять возможно больший объем. Все газы обладают большой сжимаемостью. Молекулы реальных газов обладают объемом и имеют силы взаимного притяжения, хотя эти величины весьма незначительны. В расчетах по реальным газам обычно используют газовые законы для идеальных газов. Идеальные газы — это условные газы, молекулы которых не имеют объема и не взаимодействуют друг с другом из-за отсутствия сил притяжения, а при столкновениях между ними не действуют никакие другие силы, кроме сил упругого удара. Эти газы строго следуют законам Бойля — Мариотта, Гей-Люссака и др.

Чем выше температура и меньше давление, тем поведение реальных газов ближе соответствует идеальным газам. При малых давлениях все газы можно рассматривать как идеальные. При давлениях около 100 кг/см2 отклонения реальных газов от законов идеальных газов не превышают 5 %. Поскольку отклонения реальных газов от законов, выведенных для идеальных газов, обычно ничтожны, законами для идеальных газов можно свободно пользоваться для решения многих практических задач.

Закон Бойля — Мариотта

Измерения объема газа под влиянием внешнего давления показали, что между объемом V и давлением Р имеется простая связь, выражающаяся законом Бойля — Мариотта: давление данной массы (или количества) газа при постоянной температуре обратно пропорционально объему газа:

где Р1 — давление газа при объеме V1; Р2 — давление газа при объеме V2.

Р1 * V1 = P2* V2 или Р * V= const (при t = const).

Этот постулат формулируется так: произведение давления данной массы газа на его объем постоянно, если температура не меняется (т.е. при изотермическом процессе).

Если, например, взять 8 л газа под давлением Р = 0,5 кгс/см2 и менять давление при неизменной постоянной температуре, то будут получены следующие данные: при 1 кгс/см2 газ займет объем 4 л, при 2 кгс/см2 — 2л, при 4 кгс/см2 — 1л; при 8 кгс/см2 — 0,5л.

Таким образом, при постоянной температуре всякое повышение давления приводит к уменьшению объема газа, а уменьшение объема газа — к повышению давления.

Зависимость между объемом газа и давлением при неизменной температуре широко применяется для различных расчетов в водолазной практике.

Законы Гей-Люссака и Шарля

Закон Гей-Люссака выражает зависимость объема и давления газа от температуры: при постоян-ном давлении объем данной массы газа прямо пропорционален его абсолютной температуре:

где Т1 и Т2 — температура в Кельвинах (К), которая равна температуре в °С + 273,15; т.е. 0°С ? 273 К; 100 °С — -373 К, а 0оК = -273,15 оС.

Следовательно, всякое повышение температуры приводит к увеличению объема, или, иными словами, изменение объема данной массы газа V прямо пропорционально изменению температуры t газа при постоянном давлении (т.е. при изобарическом процессе). Это положение выражается формулой:

где V1 — объем газа при данной температуре; V0 — исходный объем газа при 0°С; б — коэффициент объемного расширения газа.

При нагревании различных газов на одинаковое число градусов относительное приращение объема одинаково для всех газов. Коэффициент б является постоянной для всех газов величиной приращения объема, равной 1/273 или 0,00367 оС-1. Этот коэффициент объёмного расширения газов показывает, на какую часть объема, занимаемого при 0°С, возрастает объем газа, если его нагреть на 1°С при постоянном давлении.

Соотношение между давлением и температурой подчиняется той же закономерности, а именно: изменение давления данной массы газа прямо пропорционально температуре при неизменном объеме (т.е. при изохорном процессе: от греческих слов «изос» — равный и «хорема» — вместимость), что выражается формулой:

где Рt — давление газа при данной температуре; Р0 — исходное давление газа при 0° С; б — коэффициент объемного расширения газа.

Эта зависимость была установлена Ж.Шарлем за 25 лет до публикации Ж.Л.Гей-Люссака и нередко называется законом Шарля. Зависимость объема от температуры при постоянном давлении также была впервые установлена Шарлем.

При понижении температуры газа его давление убывает, а при температуре -273,15 °С давление любого газа равно нулю. Эта температура называется абсолютным нулем температуры. При этом прекращается хаотическое тепловое движение молекул и количество тепловой энергии становится равным нулю. Приведенные зависимости, выражающие законы Шарля и Гей-Люссака, позволяют решать важные практические задачи при подготовке и планировании подводных погружений, такие, например, как определение давления воздуха в баллонах при изменении температуры, соответствующие ему изменение запасов воздуха и времени пребывания на данной глубине и т. п.

Уравнение состояния идеального газа

Если зависимость между объемом, давлением и температурой связать воедино и выразить одним уравнением, то получается уравнение состояния идеального газа, которое объединяет законы Бойля — Мариотта и Гей-Люссака. Это уравнение впервые было выведено Б.П.Клайпероном путем преобразований уравнений, предложенных его предшественниками. Уравнение Клайперона состоит в том, что произведение давления газа данной массы на объем, деленное на абсолютную температуру, есть величина постоянная, не зависящая от состояния, в котором находится газ. Одна из форм написания этого уравнения:

В этом случае газовая постоянная r будет зависеть от природы газа. Если массой газа является моль (грамм-молекула), то газовая постоянная R является универсальной и не зависит от природы газа. Для массы газа, равной 1 молю, уравнение примет следующий вид:

Точное значение R cocтaвляeт 8,314510 Дж • моль -1 • К-1

Если брать не 1 моль, а любое количество газа, имеющего массу m, то состояние идеального газа можно выразить удобным для расчетов уравнением Менделеева — Клайперона в том виде, в котором оно было впервые записано Д.И.Менделеевым в 1874 г.:

где m — масса газа, г; М — молярная масса.

Уравнение состояния идеального газа может использоваться для расчетов в водолазной практике.

Пример. Определить, какой объем занимают 2,3 кг водорода при температуре + 10 °С и давлении 125 кгс/см2

где 2300 — масса газа, г; 0,082 — газовая постоянная; 283 — температура Т (273+10); 2 — молярная масса водорода М. Из уравнения следует, что давление, оказываемое газом на стенки сосуда, равно:

Это давление исчезает или при m > 0 (когда почти исчезает газ), или при V> ? (когда газ неограниченно расширяется), или при Т > 0 (когда молекулы газа не движутся).

Уравнение Ван-дер- Ваалъса

Еще М. В Ломоносов указывал на то, что закон Бойля — Мариотта не может быть верен при очень больших величинах давления, когда расстояния между молекулами сравнимы с их собственными размерами. Впоследствии полностью подтвердилось то, что отступления от поведения идеальных газов будут значительны при очень высоких давлениях и очень низких температурах. В этом случае уравнение идеального газа даст неверные результаты без учета сил взаимодействия молекул газа и занимаемого ими объема. Поэтому в 1873 г. Ян Дидерик Ван-дер-Ваальс предложил внести в это уравнение две поправки: на давление и на объем.

Авогадро выдвинул гипотезу, по которой при одинаковых условиях температуры и давления все идеальные газы независимо от их химической природы содержат в единице объема равное число молекул. Отсюда следует, что масса равных объемов газа пропорциональна их молекулярной массе.

Исходя из закона Авогадро, зная объемы исследуемых газов, можно определить их массу и, наоборот, по массе газа узнать его объем.

Законы газовой динамики

Закон Дальтона. Давление смеси газов равно сумме парциальных (частичных) давлений отдельных газов, составляющих смесь, т. е. тех давлений, которые производил бы каждый газ в отдельности, если бы он был взят при той же температуре в объеме смеси.

Парциальное давление газа Pr пропорционально процентному содержанию С данного газа и величине абсолютного давления Рабс газовой смеси и определяется по формуле:

где Pr — парциальное давление газа в смеси, кг/см2; С — объемное содержание газа в смеси, %.

Проиллюстрировать данный закон можно, сравнив смесь газов в замкнутом объеме с набором гирь различного веса, положенных на весы. Очевидно, что каждая из гирь будет оказывать давление на чашу весов независимо от наличия на ней других гирь.

Зависимость плотности природного газа от давления и температуры

где М  молекулярная масса газа. Для более точного определения плотности отдель­ных компонентов и смеси газов следует использовать равенства:

; ; (2.11)

где x_i  мольная доля i-го компонента; М_i  молекулярная масса i-го компонента; υ_i  объем одного моля i-го компонента.

Значения М_i и υ_i, приведены в таблице 2.2. Как видно из этой таблицы объем одного моля различных компонентов, входящих в состав природных газов, меняется от 20,87·10 -3 м 3 /моль для пентана до 22,71·10 -3 м 3 /моль для октана.

Плотность газов зависит от их состава, давления и температуры. Плотность газа при заданных давлении и температуре определяется по известной плотности при нор­мальных или стандартных условиях по формуле:

(в рабочих условиях) (2.12)

где ρ_ст  плотность газа при стандартных условиях, т.е. при Р=0,1013 МПа и Т_ст=293 К, значение которой для отдельных компонентов берется из таблицы 2.2, а при известном составе газа ρ_ст определяется по формуле:

; (2.13)

где T_ст  стандартная температура, К; Р_ат  атмосферное давление, МПа; Z  коэффициент сверхсжимаемости газа при заданных Р и Т.

Пример: где:Р = 14,71 МПа, Тст = 293К, Рат = 0,1013 МПа,Z = 0,8

При наличии влаги  водяных паров в газе, его плотность определяется по формуле:

(2.14)

где W  влагосодержание газа при условиях Р и Т, определяется согласно методам, изложенным в пункте 2.2.7; р_вп  плотность насыщенного водяного пара; Р_вп  давление насыщенного водяного пара.

Значения ρ_вп и Р_вп приведены в таблице 2.3 и показаны на рисунке 2.3. При использовании формулы (2.14) значение Z должно быть определено без учета наличия паров воды в газе.

Рисунок 2.3  Зависимости плотности ρ_вп и давления Р_вп насыщенного водяного пара от температуры.

Таблица 2.3  Зависимости плотности и давления насыщенного пара воды от температуры.

Физические свойства природного газа.

Основные параметры газа характеризуются физическими свойствами, которые зависят от температуры и давления.

2)при расчетах часто используют понятие относительной плотности:

Плотность газа при 0 и атмосферном давлении определяется:

ρ =

При умеренном давлении:

PV = RT

R – универсальная газовая постоянная. R = 8.314 кДж/кмоль·К = 8314 Дж/кмоль·К. Газы, которые подчинены этому уравнению называются идеальными.

P = ρRT , где R – газовая постоянная.

R_метан = 518,33 кДж/кг·К

R_{угл.газ} = 188,95 кДж/кг·К

R_{кислор.} = 259,81 кДж/кг·К

Реальные газы находятся под давлением. Ткр – для каждого реального газа.

Если Т меньше Ткр, то переход газа в жидком состоянии возможен.

Если Т больше Ткр невозможен ни при каком давлении.

Если Травно Ткр, то свойства жидкой и газовой фазы одинаковые.

Метан=190,55 К, Р = 4,54 МПа. Уравнение реального газа записывается с помощью Z.

Z = f(t,p) – коэффициент сжимаемости газа, учитывает отклонения газа от НГ.

Перерасчет с одних параметров на другие:

ρ = ρ₁· , где р₁ , р – абсолютное давление газа;

Z₁ , Z – коэффициент сжимаемости газа в соответствующих 2х состояниях.

Т₁ ,Т – абсолютная температура газа.

Z (р̅ , Т̅) = 1 – 0,4273·р·Т̅ˉ 3,622

X_i — объемные доли компонентов, составляющих газ.

X_i – объемная концентрация; ρ_i – плотность компонентов.

Средняя молярная масса:

Если известен массовый состав газовой смеси в %, то его среднюю молярную массу можно посчитать:

Мср= , где q_i – массовое состояние i-ого компонента в %.

При транспортировке газа различают рабочие и стандартные состояния газа:

-стандартные (t=20˚С, р=101,225Па)

Применение объема газов к стандартным условиям: V=V_газов·( ), где

ТрZ – температурный коэффициент сжимаемости при стандартных условиях;

V_газов – геометрический объем газов при стандартных условиях.

Зависимость плотности природного газа от давления и температуры

ГОСУДАРСТВЕННАЯ СЛУЖБА СТАНДАРТНЫХ СПРАВОЧНЫХ ДАННЫХ

Таблицы стандартных справочных данных

ГАЗ ПРИРОДНЫЙ РАСЧЕТНЫЙ.

ПЛОТНОСТЬ, ФАКТОР СЖИМАЕМОСТИ, ЭНТАЛЬПИЯ, ЭНТРОПИЯ, ИЗОБАРНАЯ ТЕПЛОЕМКОСТЬ, СКОРОСТЬ ЗВУКА, ПОКАЗАТЕЛЬ АДИАБАТЫ И КОЭФФИЦИЕНТ ОБЪЕМНОГО РАСШИРЕНИЯ ПРИ ТЕМПЕРАТУРАХ 250…450 К И ДАВЛЕНИЯХ 0,1…12 МПА

Tables of standard reference data. Natural gas rated. Density, compressibility factor, entalpy, entropy, isobaric specific heat, velocity of sound, index of adiabate and coefficient of volume thermal expansion in the temperature range 250…450 К and pressure range 0,1. 12 MPa

РАЗРАБОТАНЫ Всероссийским научно-исследовательским центром по стандартизации, информации и сертификации сырья, материалов и веществ Госстандарта России

АВТОРЫ: д-р техн. наук А.Д.Козлов, канд. техн. наук В.М.Кузнецов, канд. техн. наук Ю.В.Мамонов, канд. техн. наук С.А.Степанов

РЕКОМЕНДОВАНЫ К УТВЕРЖДЕНИЮ Научно-производственным объединением по исследованию и проектированию энергетического оборудования им. И.И.Ползунова; Всероссийским научно-исследовательским центром по стандартизации, информации и сертификации сырья, материалов и веществ Госстандарта России

ОДОБРЕНЫ экспертной комиссией в составе:

д-ра техн. наук В.Н.Зубарева, д-ра техн. наук Б.А.Григорьева, д-ра техн. наук В.В.Пугача, канд. техн. наук В.А.Айрапетова, канд. техн. наук П.В.Попова

ПОДГОТОВЛЕНЫ К УТВЕРЖДЕНИЮ Всероссийским научно-исследовательским центром стандартизации, информации и сертификации сырья, материалов и веществ Госстандарта России

УТВЕРЖДЕНЫ Государственным комитетом Российской Федерации по стандартизации, метрологии и сертификации «06» июля 1993 г. (протокол N 7).

ВМЕСТО ГСССД 81-84

Применение стандартных справочных данных обязательно во всех отраслях народного хозяйства

Настоящие таблицы стандартных справочных данных вводятся вместо ГСССД 81-84 [1]. Разработка новых таблиц обусловлена появлением многочисленных новых экспериментальных данных о термических свойствах природного газа [2] и разработкой более совершенной методики получения уравнений и оценки погрешностей вычисленных по нему значений [3].

Таблицы стандартных справочных данных содержат значения плотности, фактора сжимаемости, энтальпии, энтропии, изобарной теплоемкости, скорости звука, показателя адиабаты и коэффициента объемного расширения сухого природного газа, состав которого (объемные доли в процентах) регламентируется ГОСТ 23194-83: метан 98,63, этан 0,12, пропан 0,02, н-бутан 0,10, диоксид углерода 1,01, азот 0,12. Параметры состояния, при которых рассчитаны таблицы, относятся к области изменения температур и давлений, наиболее важной для практических расчетов центробежных нагнетателей для транспортирования природного газа.

Таблицы рассчитаны на основании известных термодинамических соотношений по уравнению состояния, построенному в виде зависимости свободной энергии от приведенных плотности и температуры:

где — избыточная по отношению к идеальному газу свободная энергия; 506,781 Дж/(кг К) — газовая постоянная,

и — приведенные плотность и температура; — температура, К; — плотность, кг/м ; 192,014 К и 166,695 кг/м — плотность и температура природного газа в псевдокритической точке. Значения параметров уравнения , , , , , , и представлены в таблице 1.

При заданных давлении [МПа] и температуре [К] плотность определяется в итерационном цикле методом Ньютона.

Фактор сжимаемости, энтальпия, энтропия, изобарная теплоемкость, скорость звука, показатель адиабаты и коэффициент объемного расширения рассчитывались, соответственно, по формулам:

Зависимость плотности природного газа от давления и температуры

Плотность газов

Газы в отличие от жидкостей характеризуются малой плотностью. Нормальной плотностью газа называется масса одного его литра при 0°С и давлении 1 кгс/см2. Масса одной молекулы любого газа пропорциональна его плотности.

Плотность газа с изменяется пропорционально давлению и измеряется отношением массы газа m к занимаемому им объему V:

Для практических целей различные газы удобно характеризовать по их плотности относительно воздуха при одинаковых условиях давления и температуры. Поскольку молекулы разных газов имеют различную массу, их плотности при одинаковом давлении пропорциональны молярным массам.

Плотность газов и отношение их плотности к плотности воздуха:

Плотность с, кг/м3

отношению к воздуху

Основные газовые законы

Характерным для газов является то, что они не имеют своего объема и формы, а принимают форму и занимают объем того сосуда, в который их помещают. Газы равномерно наполняют объем сосуда, стремясь расшириться и занять возможно больший объем. Все газы обладают большой сжимаемостью. Молекулы реальных газов обладают объемом и имеют силы взаимного притяжения, хотя эти величины весьма незначительны. В расчетах по реальным газам обычно используют газовые законы для идеальных газов. Идеальные газы — это условные газы, молекулы которых не имеют объема и не взаимодействуют друг с другом из-за отсутствия сил притяжения, а при столкновениях между ними не действуют никакие другие силы, кроме сил упругого удара. Эти газы строго следуют законам Бойля — Мариотта, Гей-Люссака и др.

Чем выше температура и меньше давление, тем поведение реальных газов ближе соответствует идеальным газам. При малых давлениях все газы можно рассматривать как идеальные. При давлениях около 100 кг/см2 отклонения реальных газов от законов идеальных газов не превышают 5 %. Поскольку отклонения реальных газов от законов, выведенных для идеальных газов, обычно ничтожны, законами для идеальных газов можно свободно пользоваться для решения многих практических задач.

Закон Бойля — Мариотта

Измерения объема газа под влиянием внешнего давления показали, что между объемом V и давлением Р имеется простая связь, выражающаяся законом Бойля — Мариотта: давление данной массы (или количества) газа при постоянной температуре обратно пропорционально объему газа:

где Р1 — давление газа при объеме V1; Р2 — давление газа при объеме V2.

Р1 * V1 = P2* V2 или Р * V= const (при t = const).

Этот постулат формулируется так: произведение давления данной массы газа на его объем постоянно, если температура не меняется (т.е. при изотермическом процессе).

Если, например, взять 8 л газа под давлением Р = 0,5 кгс/см2 и менять давление при неизменной постоянной температуре, то будут получены следующие данные: при 1 кгс/см2 газ займет объем 4 л, при 2 кгс/см2 — 2л, при 4 кгс/см2 — 1л; при 8 кгс/см2 — 0,5л.

Таким образом, при постоянной температуре всякое повышение давления приводит к уменьшению объема газа, а уменьшение объема газа — к повышению давления.

Зависимость между объемом газа и давлением при неизменной температуре широко применяется для различных расчетов в водолазной практике.

Законы Гей-Люссака и Шарля

Закон Гей-Люссака выражает зависимость объема и давления газа от температуры: при постоян-ном давлении объем данной массы газа прямо пропорционален его абсолютной температуре:

где Т1 и Т2 — температура в Кельвинах (К), которая равна температуре в °С + 273,15; т.е. 0°С ? 273 К; 100 °С — -373 К, а 0оК = -273,15 оС.

Следовательно, всякое повышение температуры приводит к увеличению объема, или, иными словами, изменение объема данной массы газа V прямо пропорционально изменению температуры t газа при постоянном давлении (т.е. при изобарическом процессе). Это положение выражается формулой:

где V1 — объем газа при данной температуре; V0 — исходный объем газа при 0°С; б — коэффициент объемного расширения газа.

При нагревании различных газов на одинаковое число градусов относительное приращение объема одинаково для всех газов. Коэффициент б является постоянной для всех газов величиной приращения объема, равной 1/273 или 0,00367 оС-1. Этот коэффициент объёмного расширения газов показывает, на какую часть объема, занимаемого при 0°С, возрастает объем газа, если его нагреть на 1°С при постоянном давлении.

Соотношение между давлением и температурой подчиняется той же закономерности, а именно: изменение давления данной массы газа прямо пропорционально температуре при неизменном объеме (т.е. при изохорном процессе: от греческих слов «изос» — равный и «хорема» — вместимость), что выражается формулой:

где Рt — давление газа при данной температуре; Р0 — исходное давление газа при 0° С; б — коэффициент объемного расширения газа.

Эта зависимость была установлена Ж.Шарлем за 25 лет до публикации Ж.Л.Гей-Люссака и нередко называется законом Шарля. Зависимость объема от температуры при постоянном давлении также была впервые установлена Шарлем.

При понижении температуры газа его давление убывает, а при температуре -273,15 °С давление любого газа равно нулю. Эта температура называется абсолютным нулем температуры. При этом прекращается хаотическое тепловое движение молекул и количество тепловой энергии становится равным нулю. Приведенные зависимости, выражающие законы Шарля и Гей-Люссака, позволяют решать важные практические задачи при подготовке и планировании подводных погружений, такие, например, как определение давления воздуха в баллонах при изменении температуры, соответствующие ему изменение запасов воздуха и времени пребывания на данной глубине и т. п.

Уравнение состояния идеального газа

Если зависимость между объемом, давлением и температурой связать воедино и выразить одним уравнением, то получается уравнение состояния идеального газа, которое объединяет законы Бойля — Мариотта и Гей-Люссака. Это уравнение впервые было выведено Б.П.Клайпероном путем преобразований уравнений, предложенных его предшественниками. Уравнение Клайперона состоит в том, что произведение давления газа данной массы на объем, деленное на абсолютную температуру, есть величина постоянная, не зависящая от состояния, в котором находится газ. Одна из форм написания этого уравнения:

В этом случае газовая постоянная r будет зависеть от природы газа. Если массой газа является моль (грамм-молекула), то газовая постоянная R является универсальной и не зависит от природы газа. Для массы газа, равной 1 молю, уравнение примет следующий вид:

Точное значение R cocтaвляeт 8,314510 Дж • моль -1 • К-1

Если брать не 1 моль, а любое количество газа, имеющего массу m, то состояние идеального газа можно выразить удобным для расчетов уравнением Менделеева — Клайперона в том виде, в котором оно было впервые записано Д.И.Менделеевым в 1874 г.:

где m — масса газа, г; М — молярная масса.

Уравнение состояния идеального газа может использоваться для расчетов в водолазной практике.

Пример. Определить, какой объем занимают 2,3 кг водорода при температуре + 10 °С и давлении 125 кгс/см2

где 2300 — масса газа, г; 0,082 — газовая постоянная; 283 — температура Т (273+10); 2 — молярная масса водорода М. Из уравнения следует, что давление, оказываемое газом на стенки сосуда, равно:

Это давление исчезает или при m > 0 (когда почти исчезает газ), или при V> ? (когда газ неограниченно расширяется), или при Т > 0 (когда молекулы газа не движутся).

Уравнение Ван-дер- Ваалъса

Еще М. В Ломоносов указывал на то, что закон Бойля — Мариотта не может быть верен при очень больших величинах давления, когда расстояния между молекулами сравнимы с их собственными размерами. Впоследствии полностью подтвердилось то, что отступления от поведения идеальных газов будут значительны при очень высоких давлениях и очень низких температурах. В этом случае уравнение идеального газа даст неверные результаты без учета сил взаимодействия молекул газа и занимаемого ими объема. Поэтому в 1873 г. Ян Дидерик Ван-дер-Ваальс предложил внести в это уравнение две поправки: на давление и на объем.

Авогадро выдвинул гипотезу, по которой при одинаковых условиях температуры и давления все идеальные газы независимо от их химической природы содержат в единице объема равное число молекул. Отсюда следует, что масса равных объемов газа пропорциональна их молекулярной массе.

Исходя из закона Авогадро, зная объемы исследуемых газов, можно определить их массу и, наоборот, по массе газа узнать его объем.

Законы газовой динамики

Закон Дальтона. Давление смеси газов равно сумме парциальных (частичных) давлений отдельных газов, составляющих смесь, т. е. тех давлений, которые производил бы каждый газ в отдельности, если бы он был взят при той же температуре в объеме смеси.

Парциальное давление газа Pr пропорционально процентному содержанию С данного газа и величине абсолютного давления Рабс газовой смеси и определяется по формуле:

где Pr — парциальное давление газа в смеси, кг/см2; С — объемное содержание газа в смеси, %.

Проиллюстрировать данный закон можно, сравнив смесь газов в замкнутом объеме с набором гирь различного веса, положенных на весы. Очевидно, что каждая из гирь будет оказывать давление на чашу весов независимо от наличия на ней других гирь.